
функции имеет вид
F
(
z
)=
2
iμ
4
√
z
−
1
exp
−
i
μ
2
ln
z
exp(
μ
arctg
√
z
−
1) 1 +
O
1
μ
.
(36)
Тогда аналитически продолжив выражение (36) на область
0
≤
z <
1
,
можно получить
F
(
z
) =
1
4
√
1
−
z
exp
−
i
μ
2
ln
z
4
+ ln
1 +
√
1
−
z
1
− √
1
−
z
1 +
O
1
μ
.
(37)
Асимптотика (37) является неравномерной при
z
→
1
, так как ги-
пергеометрическая функция при
z
→
1
ведет себя как
ln(1
−
z
)
, в то
время как асимптотика (37) при
z
→
1
стремится к const
/
4
√
1
−
z
.
Однако, при значениях
z
не очень близких к единице, она хоро-
шо приближает гипергеометрическую функцию
F
1
4
+
iμ
2
,
3
4
+
iμ
2
,
1 +
iμ, z
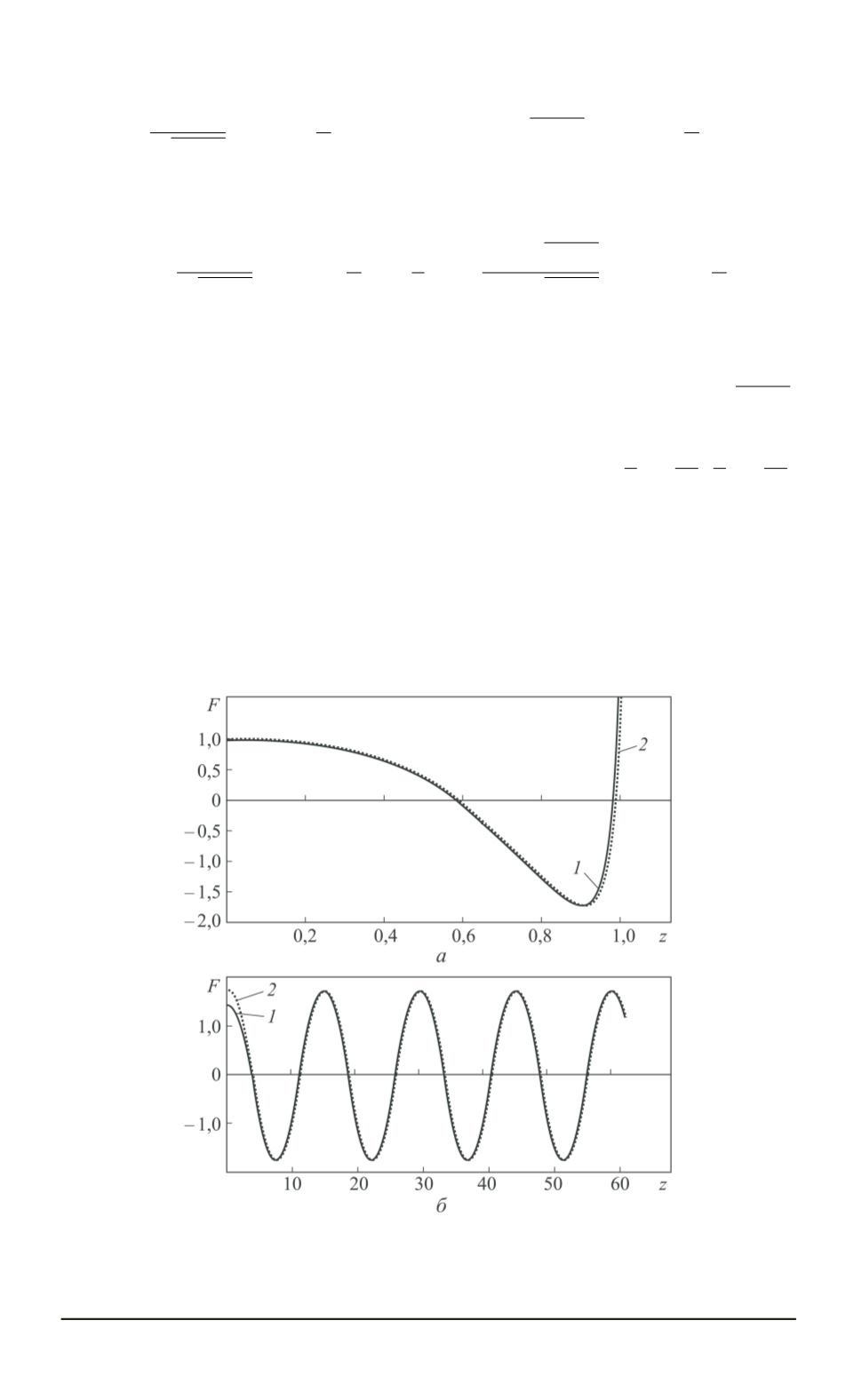
. Гипергеометрическая функция и ее ВКБ-асимптотика при
μ
= 8
приведена на рис. 5,
а
, гипергеометрическая функция и ее ВКБ-
асимптотика при
z
= 0
,
9
— на рис. 5,
б
. Очевидно, что при увели-
чении значения
μ
и соответственно уменьшении значения
z
ВКБ-
асимптотика все более точно описывает поведение гипергеометричес-
кой функции.
Рис. 5. Гипергеометрическая функция (
1
) и ВКБ-асимптотика (
2
) при
μ
= 8
(
а
)
и
z
= 0
,
9
(
б
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3
73

















