
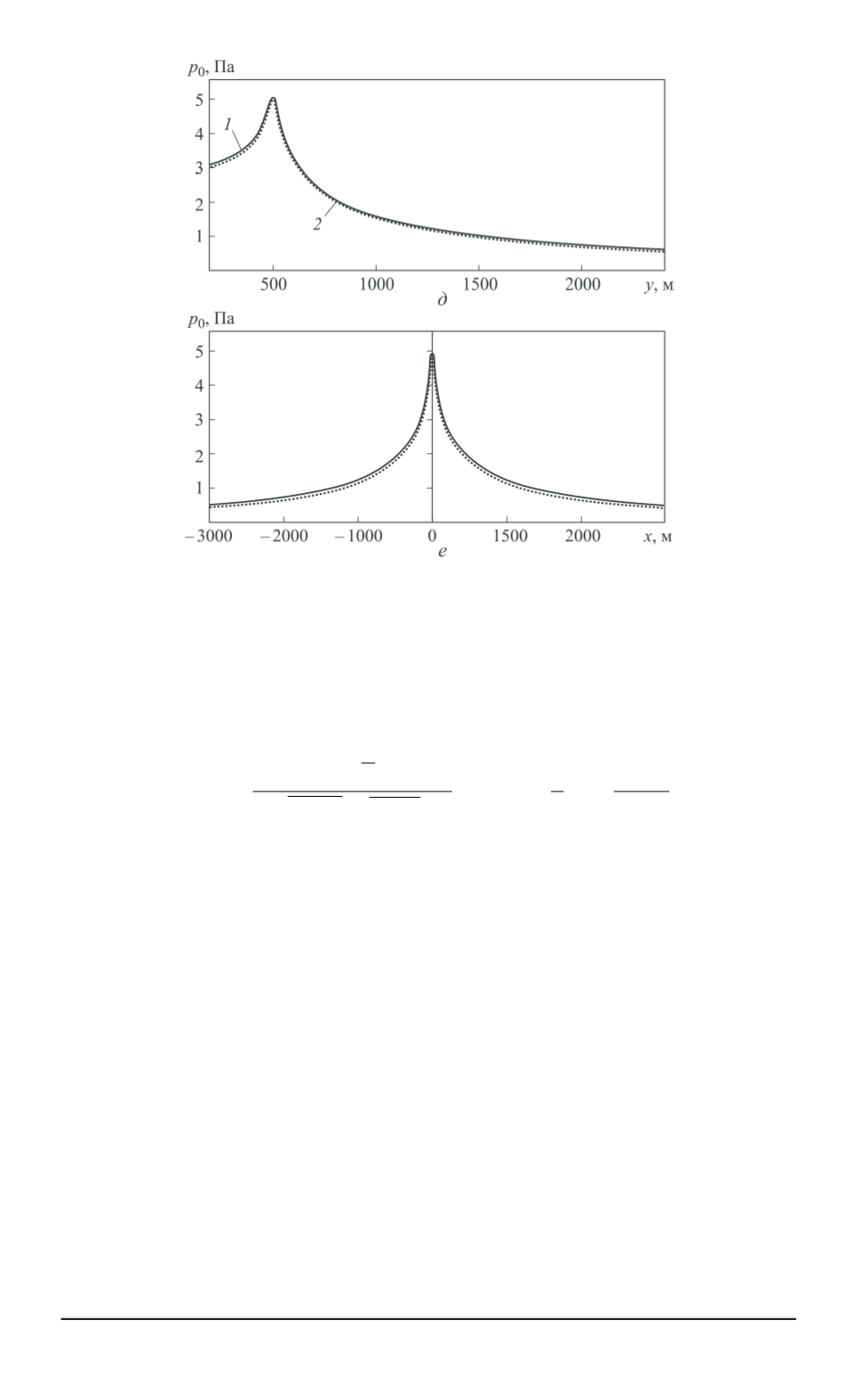
Рис. 1 (окончание). Первая (
а
,
в
), вторая (
б
,
г
) и нулевая (
д
,
е
) моды при
фиксированных значениях
x
,
z
(
а, в
),
z
,
y
(
б
,
г
):
1
— точное решение;
2
— ВКБ-асимптотика
рой имеет вид
K
(
x
)
≈
ln 4
−
ln(1
−
x
)
/
2
, окончательно записываем
выражение для асимптотики нулевой моды
p
0
(
r, ϕ, x
)
≈ −
q
√
τ
π
√
1 +
τ
√
2
r r
0
ϕ
r
ln 4
−
1
2
ln
1
−
τ
1 +
τ
.
(26)
Результаты расчетов нулевой моды для тех же исходных данных
приведены на рис. 1,
д
,
е
: срезка по переменной
y
(см. рис. 1,
д
), срез-
ка по переменной
x
(см. рис. 1,
е
). Отметим, что полное совпадение
точного и асимптотического решений имеет место в окрестности ис-
точника возмущений и существует некоторое различие вдали от него.
Это связано с тем, что асимптотика эллиптического интеграла хорошо
работает при стремлении аргумента к единице. Тем не менее в даль-
ней зоне асимптотика качественно верно описывает точное решение,
с погрешностью, не превышающей нескольких процентов.
Полное волновое поле.
Полученные выше асимптотические пред-
ставления решений для отдельных волновых мод, включая нулевую,
дают возможность перейти к вычислению полного поля внутрен-
них гравитационных волн в клине. Результат суммирования 13 мод
(включая нулевую) представлен на рис. 2, срезка по переменной
y
,
x
= 40
м,
z
=
−
40
м. Сумма асимптотик (24) бесконечного числа
волновых мод
(
n
= 1
,
2
, . . .
)
выражается через полулогарифмическую
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3
67

















