
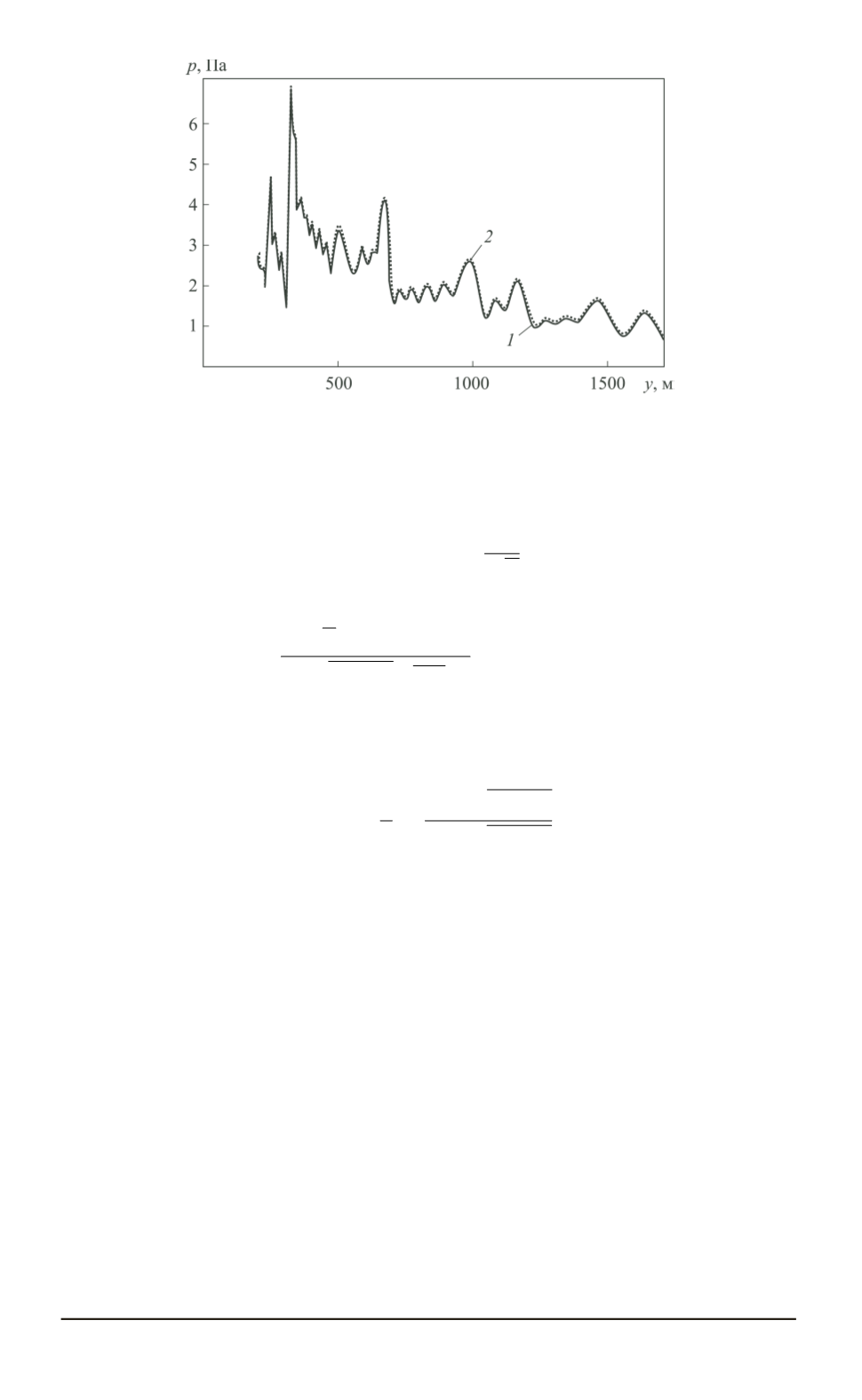
Рис. 2. Результат суммирования 13 волновых мод:
1
— точное решение;
2
— ВКБ-асимптотика
функцию индекса
3
/
2
:
Li
1
/
2
(
z
) =
∞
X
n
=1
z
n
√
n
;
∞
X
n
=1
p
n
(
r, ϕ, x
) =
−
q
√
τ
exp(
−
iπ/
4)
8
π
4
√
1
−
τ
2
√
rr
0
ϕ
r
×
×
(
Li
1
/
2
(
B
+
+
) +
Li
1
/
2
(
B
+
−
) +
Li
1
/
2
(
B
−
+
) +
Li
1
/
2
(
B
−
−
));
(27)
B
±
±
= exp(
iπ
(
±
ϕ
±
ϕ
0
+
A
(
τ
))
/ ϕ
r
);
A
(
τ
) =
1
2
ln
1
− √
1
−
τ
2
1 +
√
1
−
τ
2
.
Тогда полное волновое поле — это действительная часть выражения
(27) и нулевой моды (25). Полулогарифмическая функция в (27) обра-
щается в бесконечность в точках, где выполнено условие
π
(
±
ϕ
±
ϕ
0
+
A
(
τ
))
/ ϕ
r
= 2
πm, m
= 0
,
1
,
2
, . . .
(28)
Геометрическое место точек
(
x, y, z
)
, удовлетворяющих (28), опре-
деляет систему лучей при фиксированной одной переменной. В плос-
костях
(
y, z
)
и
(
x, z
)
решения (28) определяют пару восходящих от
источника лучей и пару нисходящих лучей с последующим их отра-
жением от наклонного дна. Теневая картина полного волнового поля
(линии уровня) в плоскости
(
y, z
)
при
x
= 40
м, остальные параме-
тры такие же, как и в предыдущих расчетах, в частности
c
= 0
,
44
,
изображена на рис. 3,
а
. Согласно представленным результатам, отче-
тливо видна лучевая структура построенных решений, в частности,
совокупность падающих и отраженных лучей. Кроме того, котангенс
68
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3

















