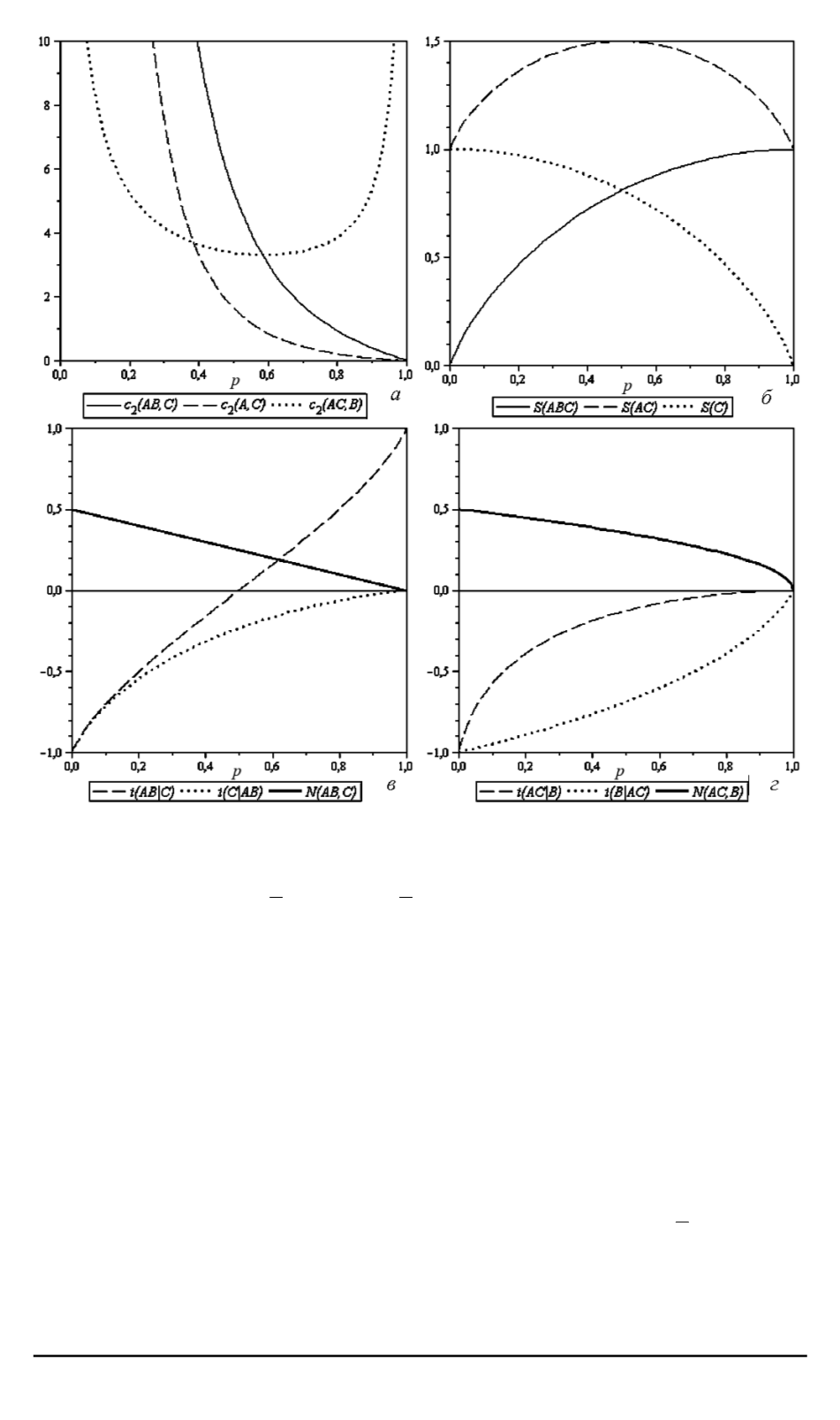
Рис. 1. Зависимость
c
2
(
a
),
S
(
б
),
i
и
N
(
в, г
) от степени диссипации
p
частицы
C
для различных звеньев состояния (6)
максимума при
p
=
1
2
, равного
3
2
(рис. 1,
б
), в то время как
S
(
B
) =
=
const
= 1
. Частица
B
всегда соответствует следствию, но величина
c
2
ведет себя немонотонно: она достигает минимума при
p
= 0
,
594
.
Чтобы объяснить это явление, отметим, что при
p
= 0
состояние (6)
чистое и, следовательно,
c
2
(
AC, B
)
→ ∞
; при
p
= 1
состояние (6)
максимально смешанное, но
S
(
AC
) =
S
(
B
)
(полностью диссипиру-
ющая частица
C
“исчезла”), поэтому вновь
c
2
(
AC, B
)
→ ∞
. Знаме-
натель выражения (3) для
c
2
(
AC, B
)
, а именно
i
AC
|
B
−
i
B
|
AC
имеет
максимум при
p
= 0
,
401
(рис. 1,
г
), в то время как числитель, предста-
вляющий собой произведение
(1
−
i
AC
|
B
)(1
−
i
B
|
AC
)
, убывает с ростом
p
, поэтому
min
c
2
смещен к большему, по сравнению с
1
2
значению
p
. Как видно на рис. 1,
a
, причинность в звене
AC
−
B
преобладает
над причинностями в других звеньях при малой степени диссипации
(
p <
0
,
387)
.
94
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 3


