
переменных после понижения порядка уравнения (9) получим
λ
dϕ
dη
−
1
η
3
1
−
ϕ
2
−
1
η
=
−
27
256
β,
(10)
где
λ
=
27
512
σα
2
e
h
α
Π
m
;
β
=
|
Δ
P
|
Π
m
,
0
≤
β
≤
1
— безразмерные критерии.
Уравнение (10) должно быть дополнено граничным условием
ϕ
= 0
, η
=
η
0
,
(11)
где
η
0
=
h
0
h
α
— величина, определяемая как минимальный действитель-
ный корень уравнения
1
η
3
1
−
1
η
=
27
256
β,
(12)
так как именно при
h
=
h
0
достигается минимальная толщина смачи-
вающей пленки (см. рис. 2).
Согласно приведенным выше оценкам, значение безразмерной тол-
щины смачивающей пленки принадлежит к интервалу
1
< η
0
<
4
/
3
.
Полагая
η
0
= 1 +
O
(
β
)
, из уравнения (12) получаем оценку
η
0
≈
1 +
27
256
β,
0
< β
1
.
(13)
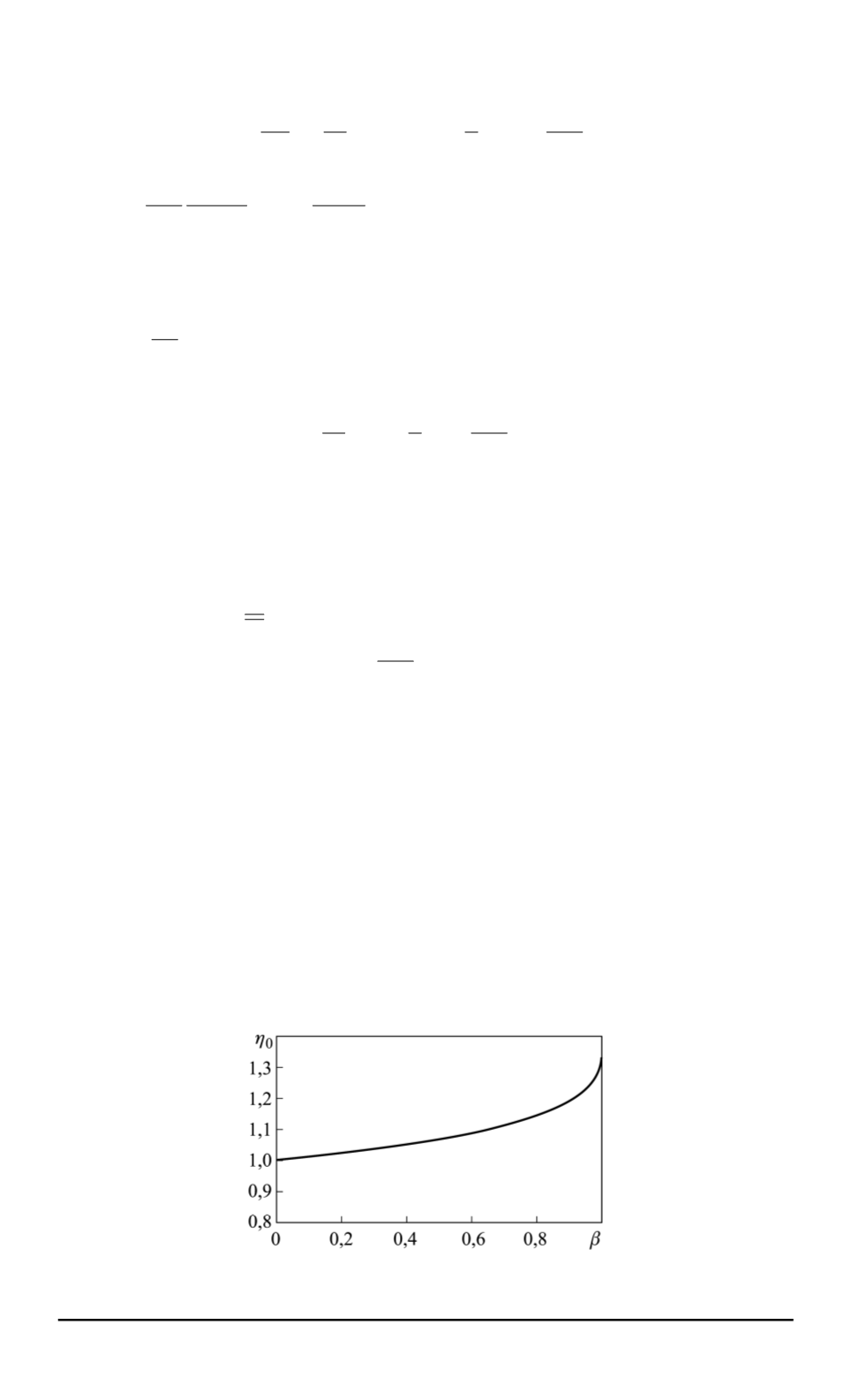
Зависимость
η
0
(
β
)
, полученная численно, приведена на рис. 3.
Характер интегральных кривых уравнения (10) может быть иссле-
дован методом изоклин. В интересующей нас области изменения пере-
менных качественный вид интегральных кривых на плоскости
(
ϕ, η
)
приведен на рис. 4. Кривая, приведенная на рис. 4,
а
, построена при
β
= 0
, а кривая, показанная на рис. 4,
б
, — при некотором произволь-
ном значении
β
в допустимом интервале изменения
0
< β <
1
.
При отсутствии отрицательного расклинивающего давления, т.е.
при
β
= 0
(см. рис. 4,
а
), на внешней границе переходного слоя от
α
-пленки к объемной части жидкости выполняется условие Юнга, так
как
ϕ
≈
1
при
η
1
. Этот факт уже был отмечен в работе [6].
Рис. 3. Полученная численно зависимость
η
0
(
β
)
128
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 1
















