
С.А. Говор, О.Н. Катков
144
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 5
ческих уравнений следует, что для многофакторной регрессионной модели ква-
зистатических испытаний необходимо провести 24 эксперимента: 12 экспери-
ментов для прямоугольного препятствия с высотами
1
H
,
2
H
и 12 эксперимен-
тов для треугольного препятствия с высотами
1
H
,
2
.
H
В общей сложности для
испытаний в статистическом и квазидинамическом режимах необходимо про-
вести 36 экспериментов.
При несоответствии линейной многофакторной модели первого порядка
заданным параметрам точности и адекватности модели порядок уравнения ре-
грессии необходимо увеличить до второго [1, 2, 10]:
2
2
0 1 1
11
1 1
1
...
...
...
.
n n
nn n
n n
y
x
x
x
x
x x
Далее следует увеличивать степень полинома до тех пор, пока аналити-
ческая зависимость полученных данных в эксперименте не достигнет желаемого
значения.
Результат планирования эксперимента.
Проанализируем полученные экс-
периментальные данные для квазидинамического режима и многофакторное
уравнение регрессии с последовательно изменяющимися степенями полинома.
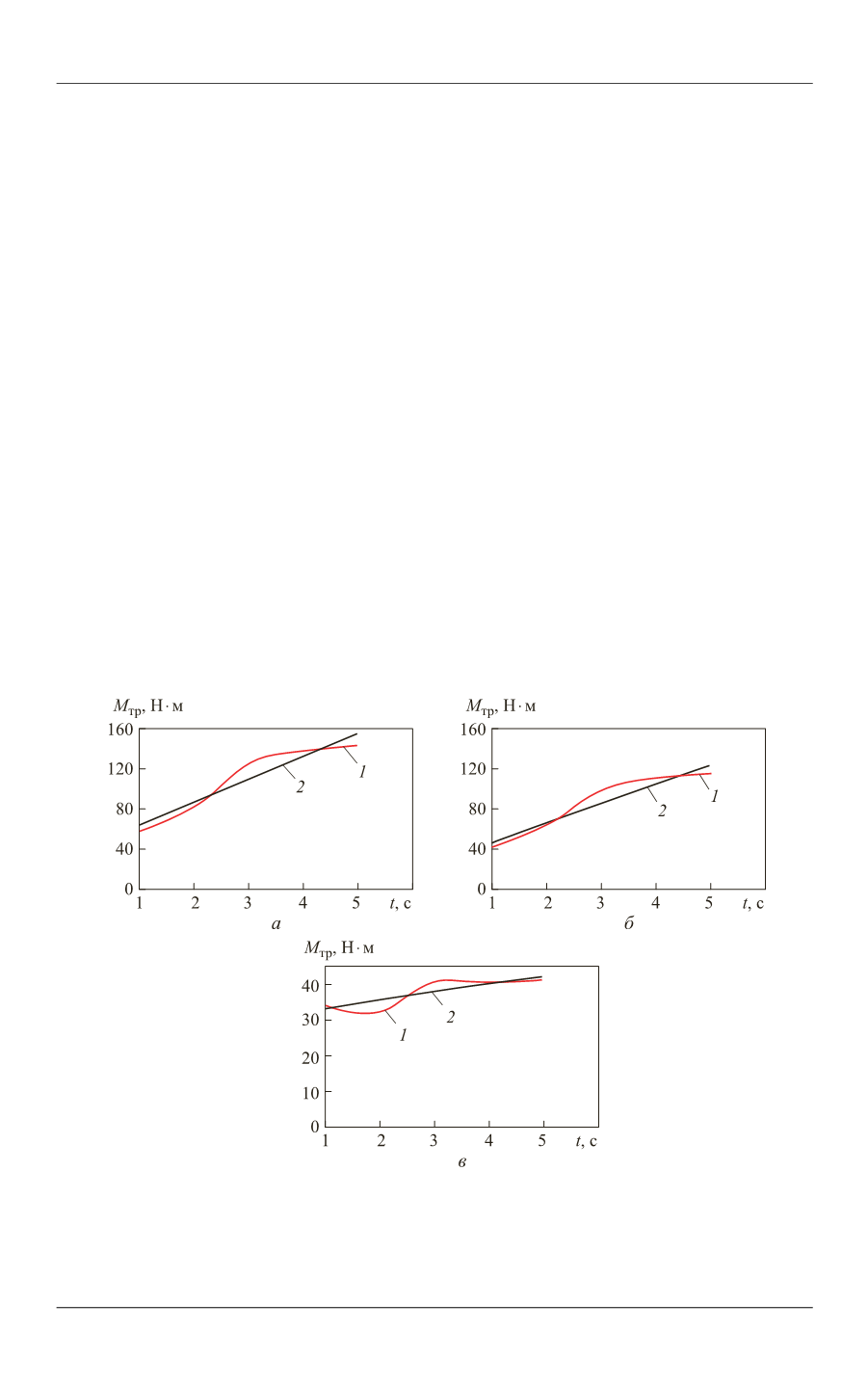
Зависимости момента трогания ЛА от времени при различных значениях дав-
ления в скегах приведены на рис. 2. В соответствии с представленными на рис. 2
зависимостями полином первого порядка плохо аппроксимирует зависимость
экспериментальных данных от времени.
Рис. 2.
Зависимость момента трогания ЛА от времени при фиксированных значениях
давления в скегах
c1
0,8
p
(
а
), 0,6 (
б
), 0,5 (
в
):
1
— экспериментальные данные;
2
— уравнение регрессии первого порядка
(аппроксимирующий полином первой степени)
















