
В.В. Дикусар, С.В. Засухин
52
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 6
Численная оптимизация проведена методом наискорейшего спуска, при этом
градиент целевой функции (5) рассчитали по формулам БАД (9), (10). Шаг вдоль
выбранного направления определяли в результате одномерной оптимизации
функции, полученной интерполяцией целевой функции с помощью сплайнов,
которые построены по 40 точкам. Итерационный процесс продолжался до тех
пор, пока чебышевская норма градиента целевой функции (5) не становилась
менее
14
1 10 .
В качестве начального управления было выбрано испарение
2
1, 0 10 ,
init
E t
0,
.
t
T
Задача численной оптимизации на всем промежут-
ке времени
0,
T
допускает декомпозицию на совокупность отдельных задач
оптимизации в соответствии с выбранным разбиением всего временного про-
межутка. В силу того, что специалисты работают с суточными данными осадков
и испарения, следовало бы рассматривать множество, состоящее из 122 задач,
соответствующих каждым суткам. Численные расчеты показали: для нахожде-
ния оптимального управления с требуемой точностью необходимо, как прави-
ло, не более 1000 итераций.
На третьем этапе численные расчеты были проведены по сценарию, анало-
гичному сценарию второго этапа, с единственным различием: целевая функция
определена по формуле (5), в которой
0
B B
и
0, 1, 2, 3 ,
A
т. е. сравнение
значений влажности почвы
, ,
z t
полученных в результате решения прямой
задачи (3) при выбранном управлении
0
,
,
n
E n B
с предписанными значениями
ˆ ,
z t
происходит в узлах сетки, принадлежащих подповерхностному слою
толщиной 3 см. В этом случае оптимизационный процесс происходил гораздо
более эффективно: во-первых, время, затрачиваемое на проведение одной итера-
ции, заметно сократилось; во-вторых, ощу-
тимо увеличилась скорость сходимости. Как
правило, оптимизационный процесс поз-
волял получить решение за 100–105 итера-
ций. Найденное оптимальное управление
opt
E
отличалось от истинного управления
true
E
незначительно:
opt
n
n
true
E t
E t
12
10, 5 10 ,
1, , .
n
N
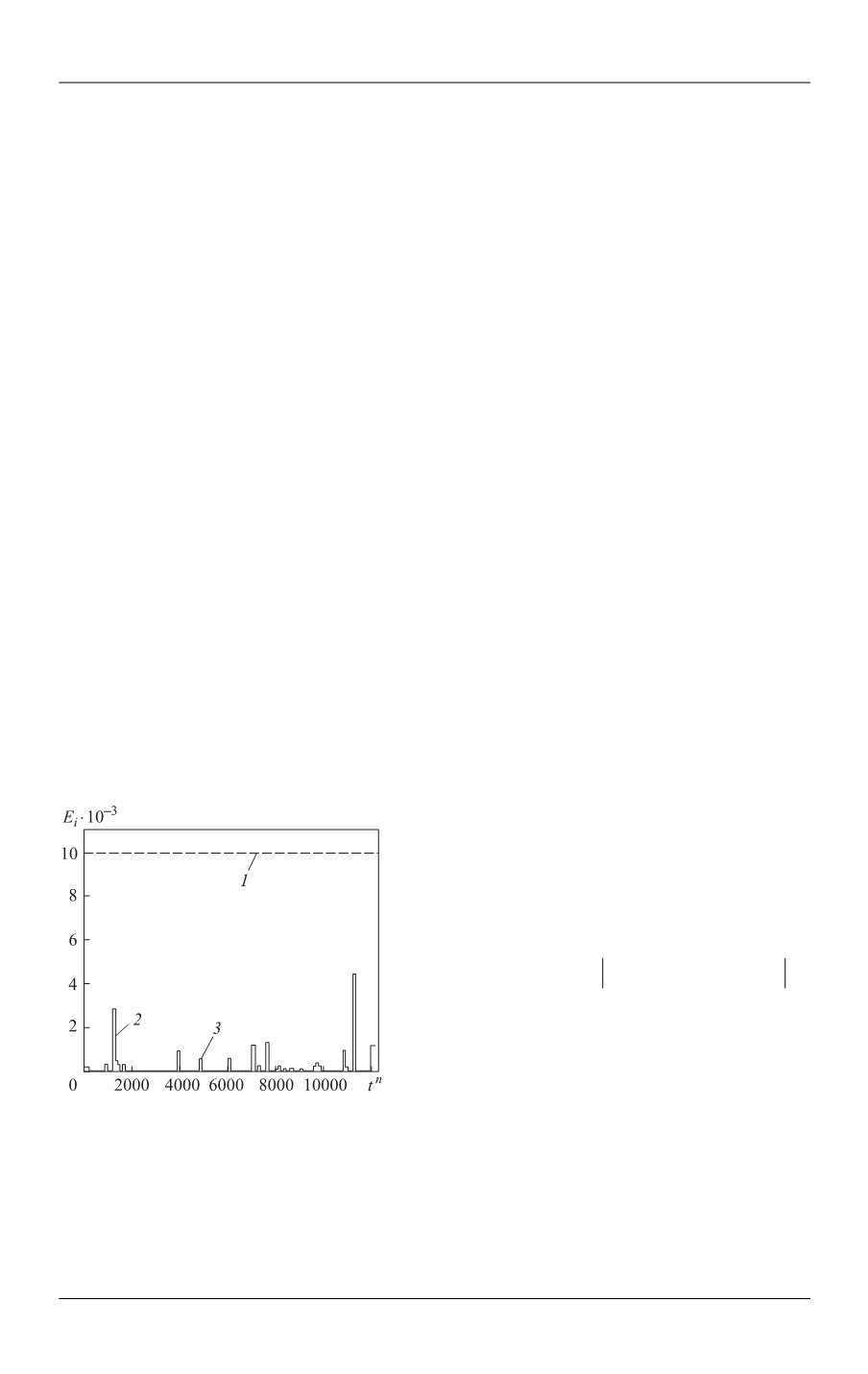
Зависимости начального, истинного
управлений и найденного с помощью чис-
ленных расчетов оптимального управления
от времени представлены на рис. 2. Зави-
симости истинного и найденного в резуль-
тате численных расчетов оптимального
управлений практически совпадают.
Заключение.
Анализ полученных результатов показал, что идея примене-
ния метода БАД при решении задачи нахождения испарения по профилям
Рис. 2.
Зависимости начального (
1
), ис-
тинного (
2
) и оптимального (
3
) управ-
лений от времени
















