
Управление синергетическими процессами…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
45
т
2
1
( )
1
0
.
( )
( )
0
2
da t
dV
a t
ba t
dt
dt
−
+
=
−
x
x
Производная, вычисляемая по этой формуле, будет отрицательно опреде-
ленной во все моменты времени при
>
( ) 0,
a t
>
( ) 0,
da t
dt
0.
b
>
(11)
Неравенства (11) выражают условия асимптотической устойчивости заслон-
ки и золотника ЭГУ при действии на них нестационарных гидродинамических
сил. В соответствии с (11) устойчивость ЭГУ зависит не только от знака сум-
марного коэффициента сил, приложенных к заслонке или к золотнику, но и от
скорости изменения этого коэффициента. Неопределенная закономерность,
которой подчиняются нестационарные гидродинамические силы, влияющие на
величину
( ),
a t
не позволяет без дополнительных исследований найти опти-
мальный алгоритм управления ЭГУ. Однако условия (11) могут быть полезны
при выборе структуры обратных связей, корректирующих динамические харак-
теристики ЭГУ.
С учетом изложенного выше синтез алгоритмов управления нелинейными
гидросистемами является очень сложной задачей, конкретные решения которой
требуют проведения численных экспериментов на ЭВМ. Чтобы такие экспери-
менты были целенаправленными, необходимо сначала определить алгоритмы
оптимального управления линейными динамическими гидросистемами, а затем
скорректировать полученные результаты с учетом реальных для данной систе-
мы нелинейностей [14].
В некоторых случаях первая часть задачи может быть решена аналитически.
Например, при применении ПИ-регулятора в системе с насосом легко постро-
ить структурную схему, изображенную на рис. 3.
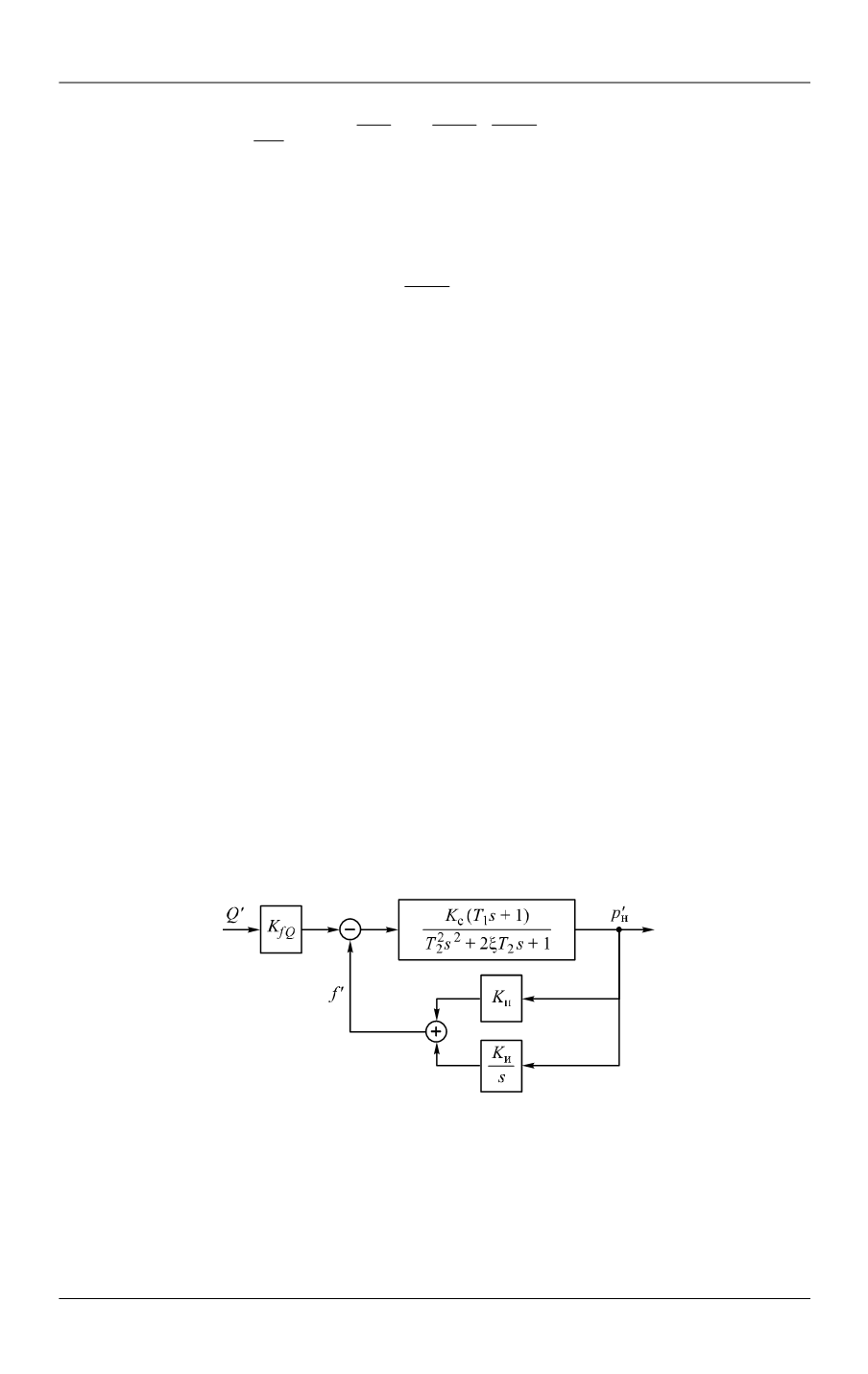
Рис. 3.
Структурная схема гидросистемы с насосом и ПИ-регулятором:
пр
K
— коэффициент усиления пропорциональной составляющей алгоритма, формируемого
ПИ-регулятором;
и
K
— интегральная составляющая того же алгоритма
Характеристическое уравнение системы, записанное в предложенной Выш-
неградским форме, имеет вид
















