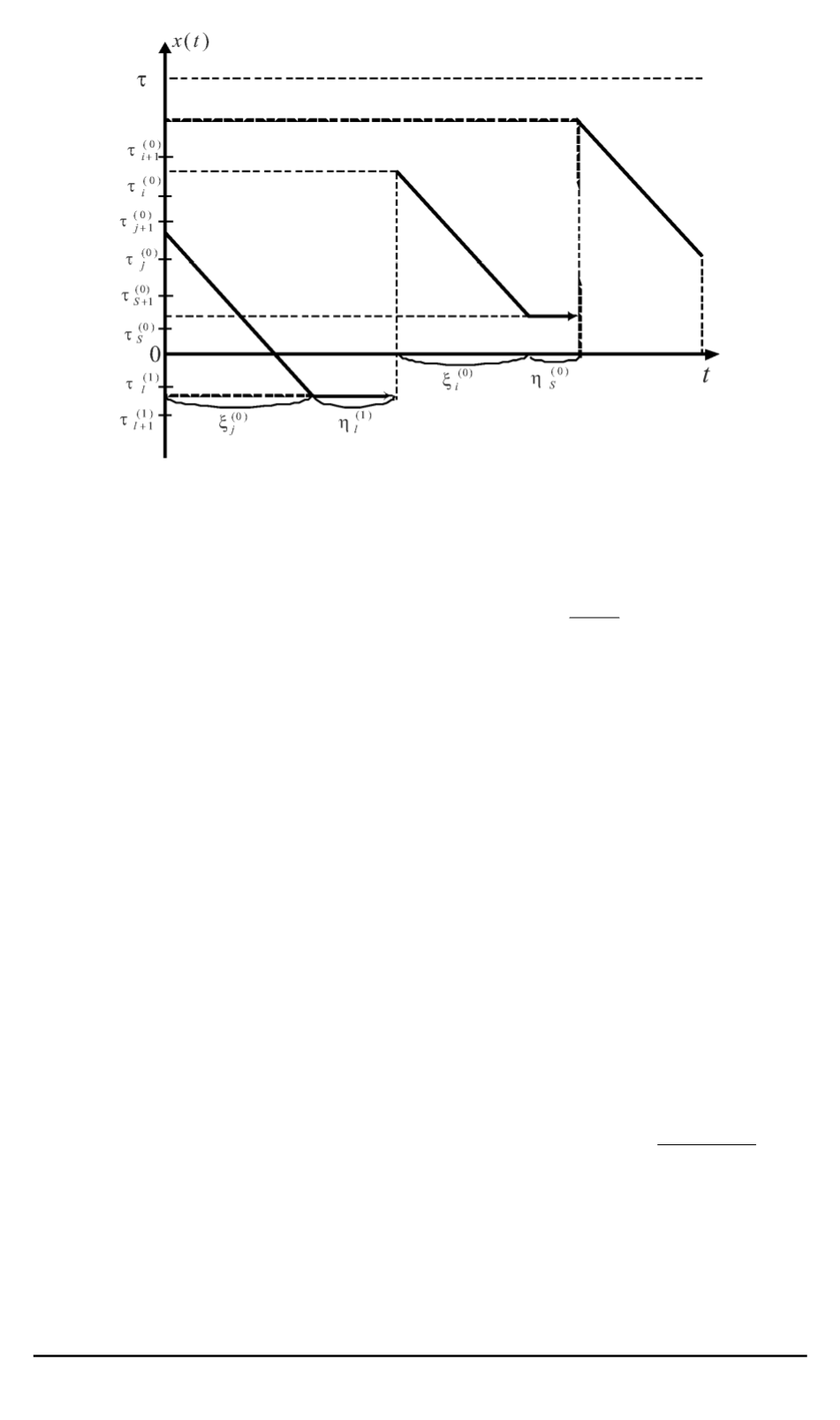
Пример траектории случайного процесса
x
(
t
)
, описывающего объем запаса
продукта
помощью соотношения
ζ
(
t
) =
ζ
n
, t
n
≤
t < t
n
+1
, n
= 0
,
∞
.
Случайный процесс
ζ
(
t
)
, t
≥
0
, представляет собой управля-
емый полумарковский процесс с конечным множеством состояний
E
=
{
0
,
1
, . . . , N
0
−
1
}
, траектории которого непрерывны справа. По-
следовательность
{
ζ
n
}
∞
n
=0
является цепью Маркова, вложенной в этот
процесс. Управление процессом
ζ
(
t
)
осуществляется в моменты вре-
мени
t
n
(после определения значения процесса
x
(
t
n
)
).
Параметр управления
u
n
— случайная величина, характеризующая
длительность периода времени до момента следующего заказа на по-
полнение запаса. Если
ζ
n
=
k
, то
u
n
=
ξ
(0)
k
(равенство случайных
величин понимается как совпадение функций распределения). Мно-
жество допустимых значений параметра управления
U
совпадает с
множеством неотрицательных чисел,
U
= [0
,
∞
)
.
Задача оптимизации управления запасом в этой стохастической
модели, или задача управления построенным сопровождающим по-
лумарковским процессом, заключается в выборе управляющих веро-
ятностных распределений
G
(0)
k
(
t
) =
P ξ
(0)
k
< t
,
k
= 0
, N
0
−
1
, до-
ставляющих экстремум некоторому показателю качества управления
I
(
G
(0)
0
(
∙
)
, G
(0)
1
(
∙
)
, . . . , G
(0)
N
0
−
1
(
∙
))
.
3. Стационарный стоимостной функционал. Вероятностные и
стоимостные характеристики модели.
Для того чтобы формально
поставить задачу оптимального управления в стохастической модели
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 3
67


