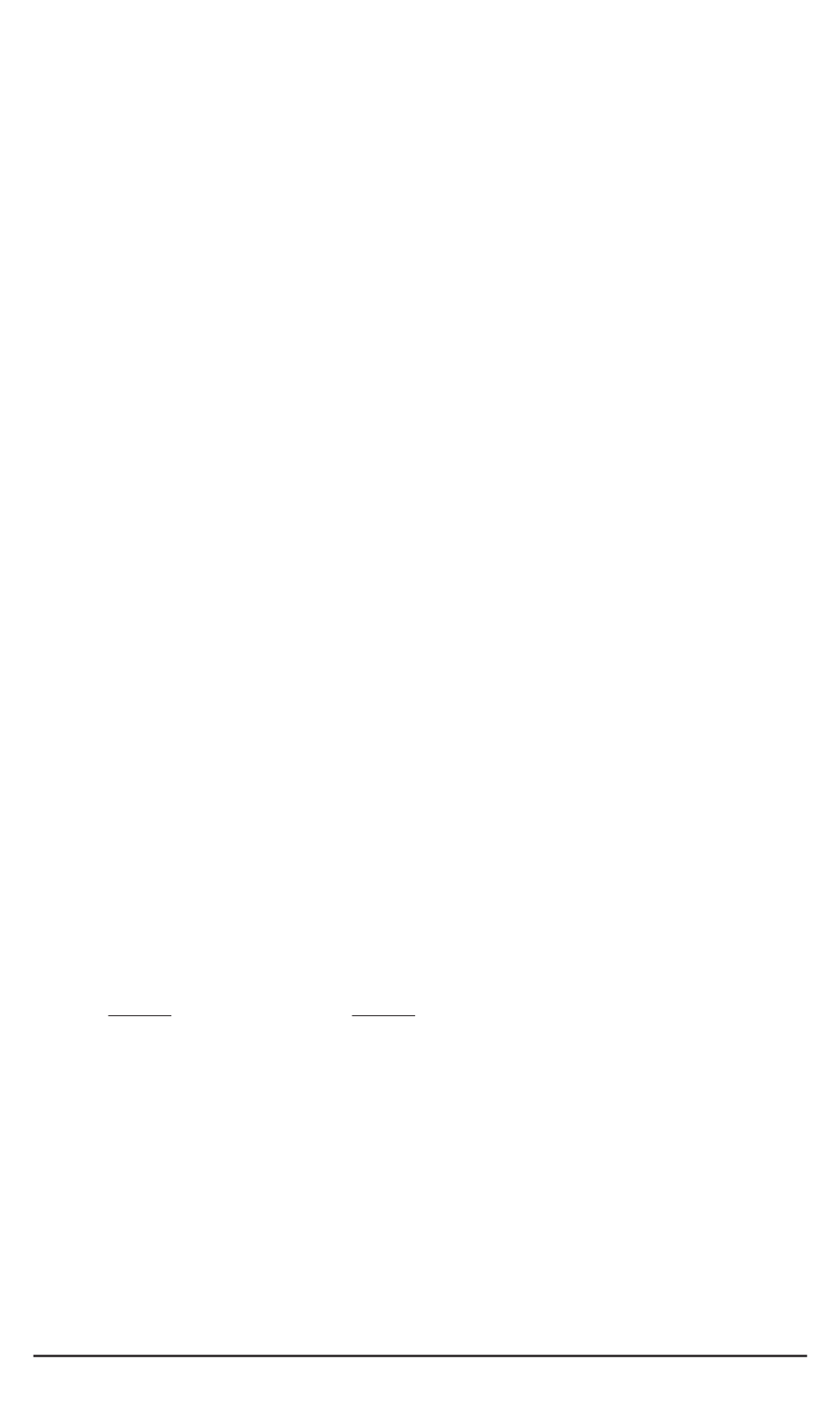
Из (43) следуют обобщенные уравненияПуассона дляопределения
тензора
Q
˙Q +W
·
Q = 0
.
(57)
Первые интегралы при отсутствии внешних сил.
Вопросы на-
хожденияпервых интегралов уравнений (56) при различных допу-
щениях о виде моментов внешних сил
˜
μ
αβ
рассматривались в ряде
работ [15–18] . Покажем, что полученные тензорные формы (54) и
(48) уравненияизменениямомента импульса иногда более предпочти-
тельны, чем компонентнаяформа (56), поскольку позволяют получить
явные представления первых интегралов.
Пусть момент внешних сил
n
−
2
˜
μ
равен нулю. Поиск ненулевого
решенияуравнений (56) в этом случае далеко не очевиден. В то же
времятензорное уравнение (48) имеет очевидное решение
(W
т
·
I)
· ·
n
э
=
n
−
2
b
,
(58)
где
n
−
2
b
— постоянный (не зависящий от времени) тензор (
n
−
2
)-го
ранга, компоненты
b
i
3
...i
n
этого тензора в неподвижном базисе
e
j
также
не зависят от времени, а в подвижном
¯e
i
являются функциями от
t
:
n
−
2
b =
b
i
3
...i
n
(
t
)¯e
i
3
(
t
)
⊗
. . .
⊗
¯e
i
n
(
t
) =
b
i
3
...i
n
e
i
3
⊗
. . .
⊗
e
i
n
. Если заданы
начальные данные
t
= 0 :
x
0
=
x
0
0
, v
0
=
v
0
0
, v
=
v
0
,
n
−
2
¯
m
=
n
−
2
¯
m
0
≡
◦
V
◦
ρx
×
v
0
d
◦
V ,
(59)
то можно явным образом найти
n
−
2
b =
n
−
2
¯
m
0
−
Mx
0
0
×
v
0
0
.
Умножим уравнения(58) на тензор
n
э
, тогда получим следующее
алгебраическое уравнение относительно тензора
W
:
(W
т
·
I)
· ·
(Δ
II
−
Δ
III
) = b
,
(60)
при этом
b =
1
k
(
n
−
2)
n
−
2
b
. . .
n
−
2
·
n
э
=
1
k
(
n
−
2)
(
n
−
2
¯m
0
0
−
M
x
0
0
×
v
0
0
)
. . .
n
−
2
·
n
э
;
(61)
b =
b
ij
e
i
⊗
e
j
=
b
ij
(
t
)¯e
i
(
t
)
⊗
¯e
j
(
t
);
(62)
k
(
n
−
2)
b
ij
=
J
ij
0
−
J
ji
0
−
M
(
x
0
i
0
v
0
j
0
−
x
0
j
0
v
0
i
0
);
(63)
b
kl
(
t
) =
b
ij
Q
k
i
(
t
)
Q
l
j
(
t
)
,
(64)
где
x
0
0
=
x
0
i
0
e
i
,
v
0
0
=
v
0
i
0
e
i
,
J
ij
0
=
◦
V
◦
ρx
i
v
j
0
d
◦
V
. Записываяуравнение
(60) в подвижном базисе, с учетом соотношений (64) получаем явное
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3
69