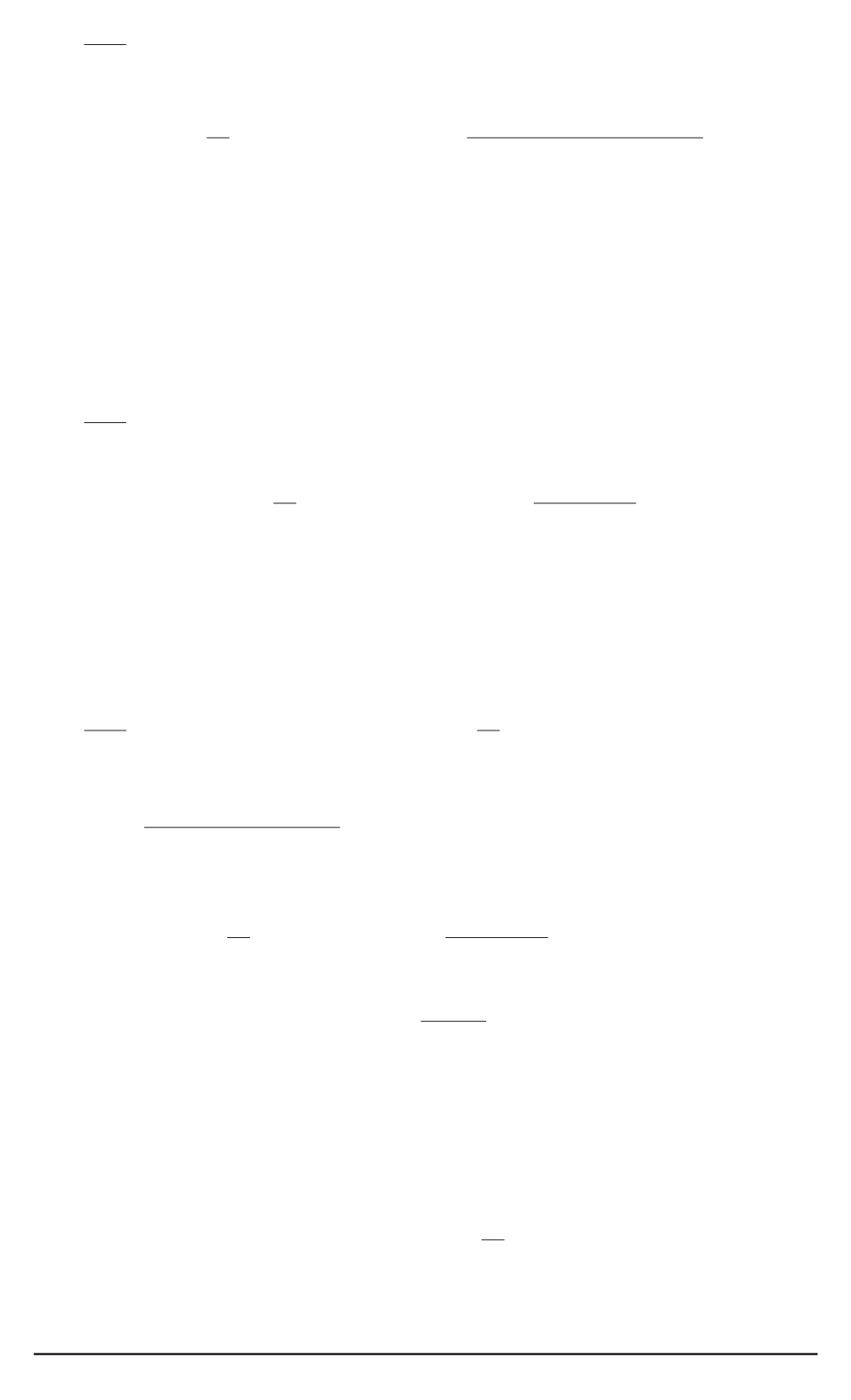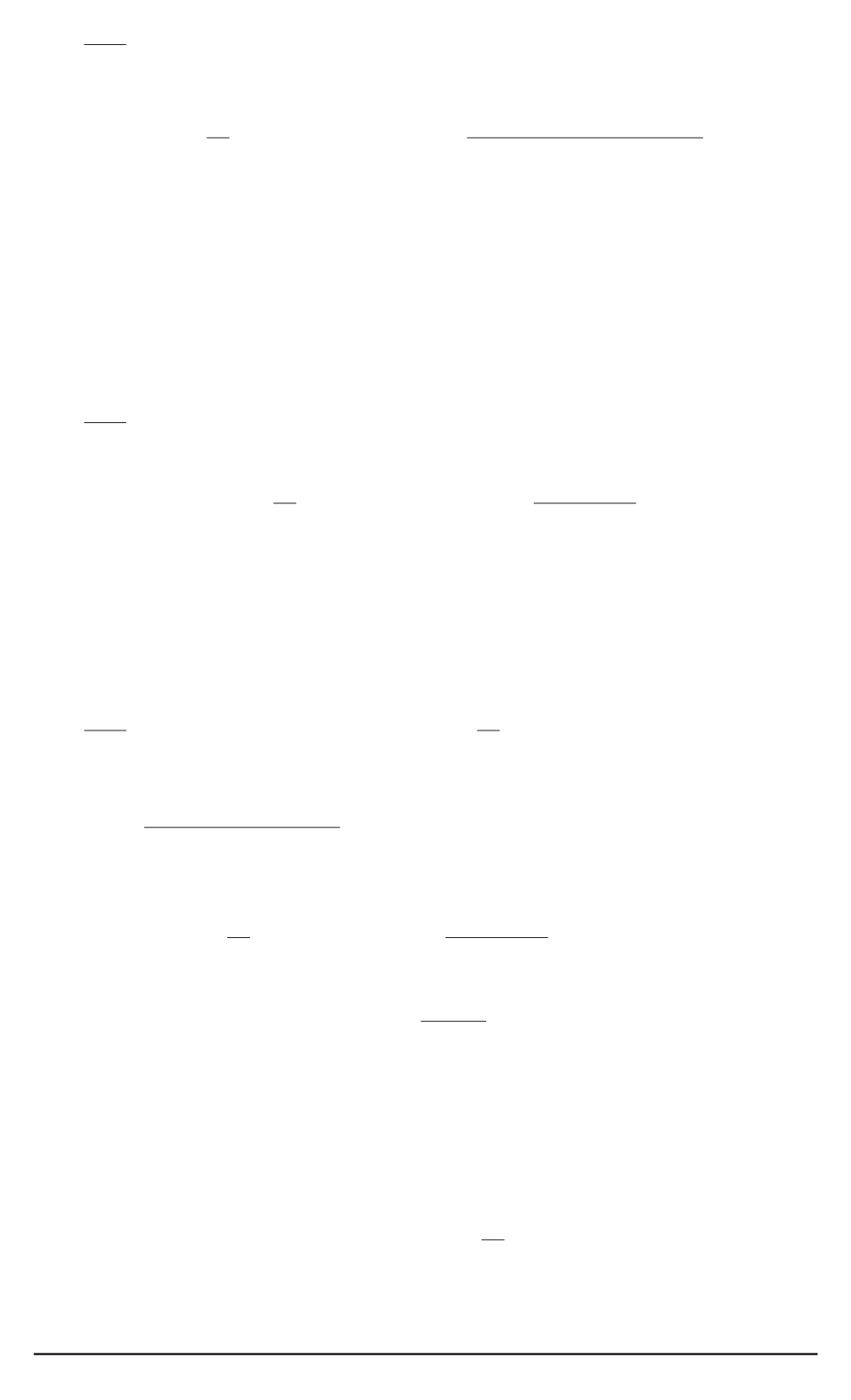
∂
m
∂t
m
A
[
u
(
x, t
)]
t
=0
A
[
ϕ
(
r
)] =
=
m
+1
n
=0
1
n
!
A
(
n
)
[
ϕ
(
r
)]
n
z
=1
k
1
,...,k
n
m
!
k
1
!
. . .
(
k
z
−
1)!
. . . k
n
!
×
×
A
[
k
1
]
[
ϕ
(
r
)]
. . . A
[
k
z
]
[
ϕ
(
r
)]
. . . A
[
k
n
]
[
ϕ
(
r
)]
.
(28)
В соотношении (28) сумма берется по всем
k
i
, удовлетворяющим усло-
вию
k
1
+
. . .
+
k
n
=
m
+ 1
. Если умножить и разделить множитель
m
!
на
k
z
, получим
∂
m
∂t
m
A
[
u
(
x, t
)]
t
=0
A
[
ϕ
(
r
)] =
=
m
+1
n
=0
1
n
!
A
(
n
)
[
ϕ
(
r
)]
n
z
=1
k
1
,...,k
n
m
!
k
z
k
1
!
. . . k
n
!
×
×
A
[
k
1
]
[
ϕ
(
r
)]
. . . A
[
k
z
]
[
ϕ
(
r
)]
. . . A
[
k
n
]
[
ϕ
(
r
)]
или, по-другому,
∂
m
∂t
m
A
[
u
(
x, t
)]
t
=0
A
[
ϕ
(
r
)] =
m
+1
n
=0
1
n
!
A
(
n
)
[
ϕ
(
r
)]
×
×
k
1
,...,k
n
m
! (
k
1
+
. . .
+
k
n
)
k
1
!
. . . k
n
!
A
[
k
1
]
[
ϕ
(
r
)]
. . . A
[
k
z
]
[
ϕ
(
r
)]
. . . A
[
k
n
]
[
ϕ
(
r
)] =
=
m
+1
n
=0
1
n
!
A
(
n
)
[
ϕ
(
r
)]
k
1
,...,k
n
(
m
+ 1)!
k
1
!
. . . k
n
!
A
[
k
1
]
[
ϕ
(
r
)]
. . .
. . . A
[
k
z
]
[
ϕ
(
r
)]
. . . A
[
k
n
]
[
ϕ
(
r
)] =
∂
m
+1
∂t
m
+1
A
{
exp (
t A
) [
ϕ
(
r
)]
}
t
=0
.
(29)
Таким образом, соотношение (24) выполняется, что, в свою оче-
редь, в силу метода математической индукции делает справедливым
равенство (23) для любого
m
. В этом случае можно записать ряд Тей-
лора по степеням переменной
t
правой части (17)
A
{
exp (
t A
) [
ϕ
(
r
)]
}
=
∞
n
=0
1
n
!
t
n
A
[
n
+1]
[
ϕ
(
r
)]
или, по-другому,
10
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 4