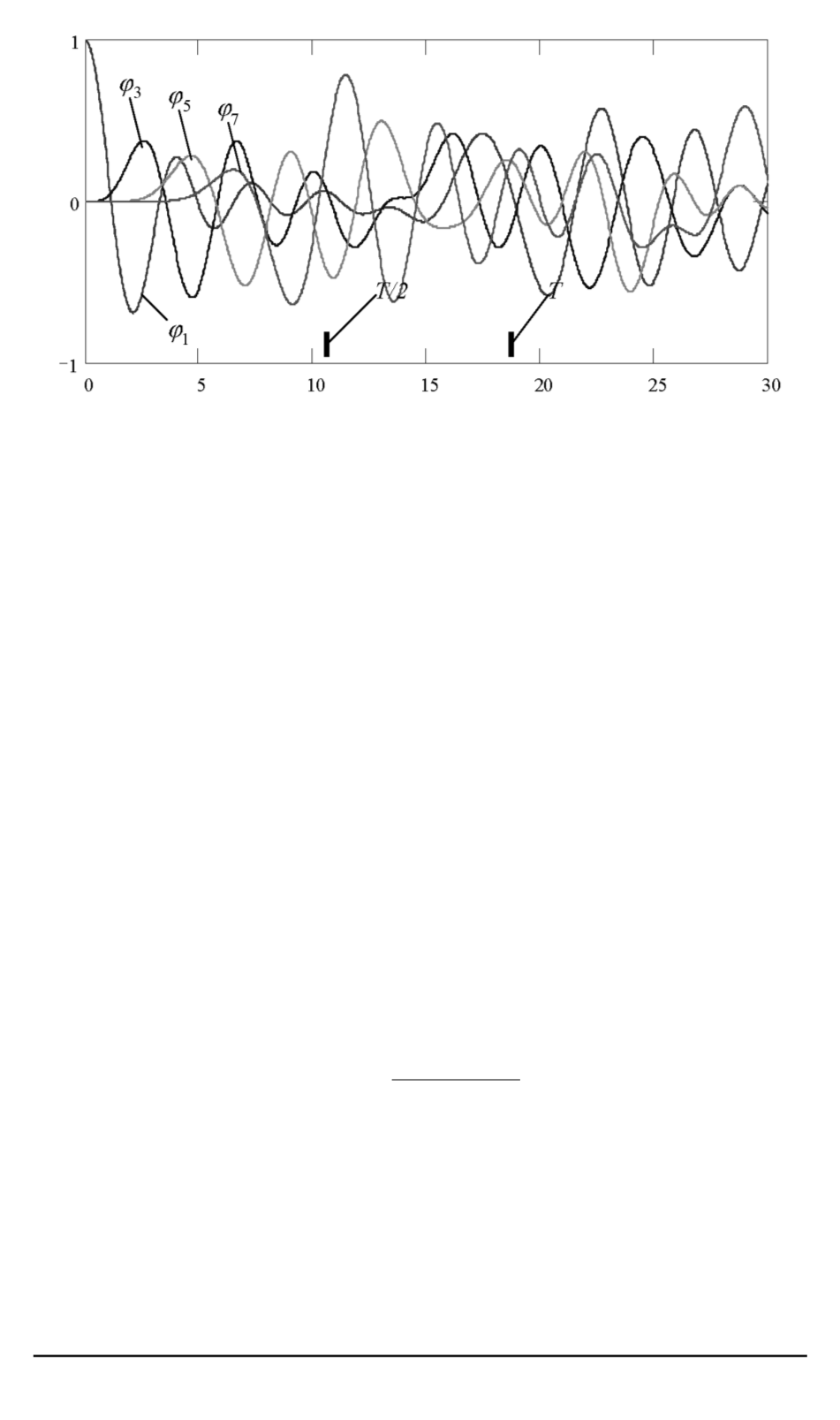
Рис. 8. Графики отклонений масс дискретной системы
системы движению, полученному интегрированием дифференциаль-
ных уравнений, может быть только в случае, когда начальные условия
(координаты и скорости) пропорциональны коэффициентам распреде-
ления амплитуд формы колебаний. Это объясняется тем, что в такой
механической системе образуется стоячая волна, в которой не про-
исходит переноса энергии и, следовательно, отсутствуют связанные с
этим волновые явления.
Выводы.
1. Для низших собственных частот сами частоты и от-
клонения масс квазиоднородной системы совпадают с частотами и от-
клонениями соответствующих сечений непрерывной однородной си-
стемы. С увеличением номера частоты различия становятся более за-
метными. Частоты однородной системы кратны первой частоте, а в
квазиоднородной системе они подчиняются закону дисперсии. Откло-
нения сечений однородной системы составляют ряд Фурье, а в квази-
однородной системе должны удовлетворять системе алгебраических
уравнений.
2. Форма колебаний дискретной квазиоднородной системы соста-
вляет неотъемлемую часть моды однородной непрерывной системы и
может быть определена по формуле
β
k
1
−
i
=
sin (
kπi
/
N
)
sin (
kπ
/
N
)
,
где
k
— номер собственной частоты;
i
— номер сечения;
N
— число
участков.
3. В течение первого полупериода колебаний движение квазиодно-
родной системы при данном начальном условии несколько напомина-
ет движение непрерывной однородной системы. В каждом следующем
полупериоде характер движения этих двух систем существенно раз-
личается из-за различия в частотах и амплитудах масс и сечений.
64
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 3


