выражением
u
(
x, t
) =
A
1
sin
ωt
−
2
πx
λ
+
A
2
sin
ωt
+
2
πx
λ
=
= (
A
1
−
A
2
) sin
ωt
−
2
πx
λ
+
A
2
sin
ωt
−
2
πx
λ
+
+
A
2
sin
ωt
+
2
πx
λ
= (
A
1
−
A
2
) sin
ωt
−
2
πx
λ
+
+ 2
A
2
cos
2
πx
λ
sin
ωt.
Таким образом, если амплитуды прямой и отраженной волны раз-
личны, то, следовательно, энергия может переноситься бегущей вол-
ной по среде, в которой они распространяются.
Для решения одномерного волнового уравнения (2) при соответ-
ствующих начальных и краевых условиях можно использовать метод
Даламбера (метод характеристик и построение прямых и обратных
волн) либо метод Фурье (метод разделения переменных и разложение
решения по собственным функциям) [2]. Сравним эти методы решения
на примере.
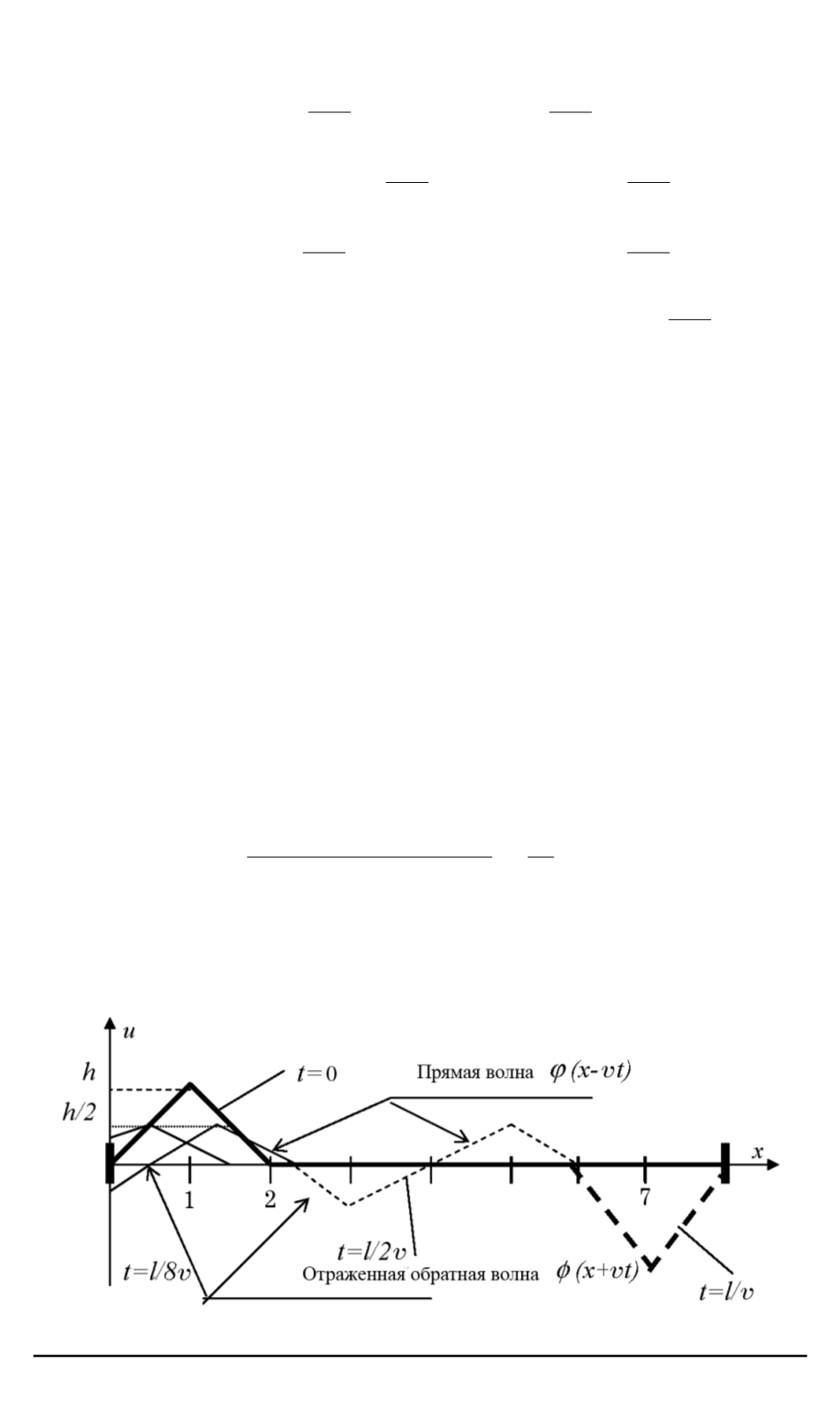
Рассмотрим колебания струны (рис. 2) с закрепленными концами
x
= 0
и
x
=
l
. Начальные скорости точек равны нулю, а начальное
отклонение имеет форму треугольника с вершиной в точке
x
=
l/
8
и
высотой
h
.
Решение уравнения колебаний струны методом Даламбера имеет
вид
u
(
x, t
) =
f
(
x
−
at
) +
f
(
x
+
at
)
2
+
1
2
a
x
+
at
Z
x
−
at
F
(
x
)
dx.
Для построения формы струны разобьем первоначальный профиль
струны на прямую и обратную волны с максимальным отклонением
Рис. 2. Формы колебаний струны
54
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 3


