стемы методом остатка, а также по формуле (17), имеют одинако-
вые значения
ω
1
= 0
,
3902
,
ω
2
= 0
,
7654
,
ω
3
= 1
,
1111
,
ω
4
= 1
,
4142
,
ω
5
= 1
,
6629
,
ω
6
= 1
,
8478
,
ω
7
= 1
,
9616
. Этим же методом остатка
определены коэффициенты распределения амплитуд форм колебаний.
Коэффициенты формы колебаний для 7-й собственной частоты совпа-
дают со значениями отклонений 7-й моды, рассчитанными для семи
сечений (см. рис. 3). Такое же сравнение коэффициентов формы ко-
лебаний остальных собственных частот показало полное совпадение
непрерывной однородной и квазиоднородной систем.
Величины отклонений масс
ϕ
i
для соответствующих собственных
частот при
t
= 0
и при нулевых начальных условиях, кроме
ϕ
1
= 1
,
полученные по формам собственных колебаний решением системы
алгебраических уравнений, приведены в табл. 2.
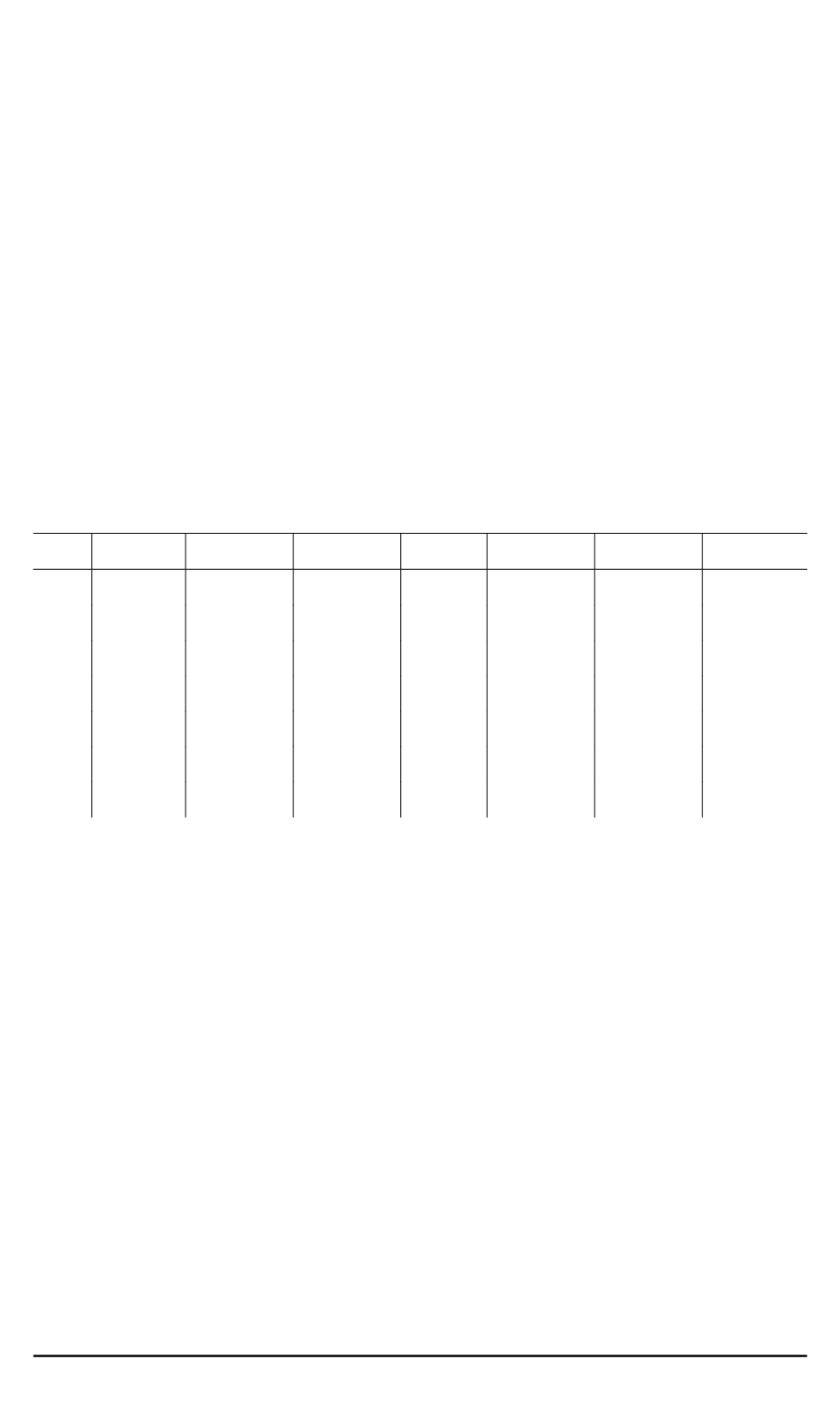
Таблица 2
ω
1
ω
2
ω
3
ω
4
ω
5
ω
6
ω
7
ϕ
1
0,0366 0,125
0,2134 0,25 0,2134
0,125
0,0366
ϕ
2
0,0676 0,1768 0,1633
0
– 0.1633 – 0.1768 – 0,0676
ϕ
3
0,0884 0,125 -0,0884 – 0,25 – 0,0884 0,125
0,0884
ϕ
4
0,0957
0
– 0,231
0
0,231
0
– 0,0957
ϕ
5
0,0884 – 0,125 – 0.0884 0,25 – 0,0884 – 0,125 0,0884
ϕ
6
0,0676 – 0,1768 0,1633
0
– 0,1633 0,1768 – 0,0676
ϕ
7
0,0366 – 0,125 0,2134 – 0,25 0,2134 – 0,125 0,0366
Установленные амплитуды главных колебаний позволяют постро-
ить графики зависимости от времени отклонений 1, 3, 5 и 7-й масс
(рис. 8) рассмотренной механической системы.
Сравнение графиков на рис. 4 и 8 показывает, что некоторые вол-
новые особенности в дискретной системе проявляются только в тече-
ние первого полупериода движения со значительными искажениями
(несоответствие значений амплитуд колебаний масс) по отношению к
однородной непрерывной системе. Дальнейшее движение квазиодно-
родной системы в корне отличается от движения однородной системы
и от движения масс в экспериментальной установке. Как указывалось
ранее, это объясняется тем, что собственные частоты (и тем самым фа-
зы колебаний) квазиоднородной системы не кратны первой собствен-
ной частоте, косинусы в уравнениях не меняют одновременно знак
на обратный по прошествии полупериода и отражения волны не про-
исходит. Соответствие реального движения дискретной однородной
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 3
63


