В соответствии с законом дисперсии для струны, закрепленной с
обеих сторон, получаем формулу для круговой частоты
ω
=
vK
=
v
π
N
.
Разделив всю струну на 8 характерных участков и приняв фазовую
скорость
v
= 1
участок/с и волновое число
K
= 2
π/λ
(
λ
= 2
N
для струны, закрепленной с двух сторон), выразим отклонение
i
-го
сечения для
k
-й собственной частоты:
u
k
=
A
k
sin
kπi
8
cos
kπt
8
.
(12)
Тогда круговая частота первого тона колебаний
ω
1
=
π/
8 =
= 0
,
3927
с
−
1
, а следующие шесть частот будут кратны первому то-
ну и равны
ω
2
= 0
,
7854
,
ω
3
= 1
,
1781
,
ω
4
= 1
,
5708
,
ω
5
= 1
,
9635
,
ω
6
= 2
,
3562
,
ω
7
= 2
,
7489
c
−
1
. Aмплитуды семи первых мод, или соб-
ственных функций, равны
А
1
= 0
,
09445
,
А
2
= 0
,
16787
,
А
3
= 0
,
29546
,
А
4
= 0
,
20264
,
А
5
= 0
,
16567
,
А
6
= 0
,
19872
,
А
7
= 0
,
04871
. Значения
отклонений
u
i
семи сечений для первых семи гармоник при
t
= 0
и
h
= 1
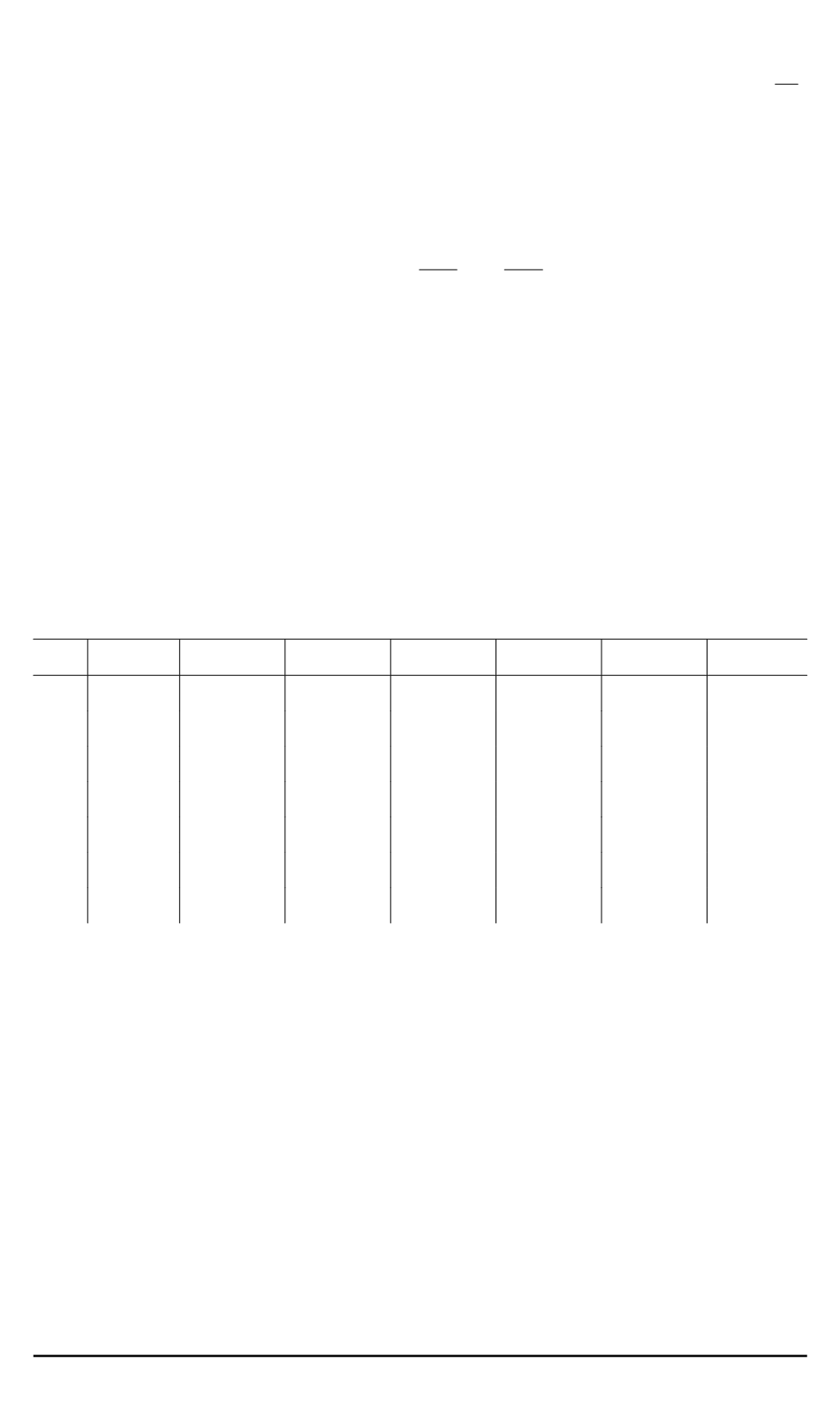
, вычисленные по формуле (12), приведены в табл. 1.
Таблица 1
ω
1
ω
2
ω
3
ω
4
ω
5
ω
6
ω
7
u
1
0,0361 0,1187 0,1898 0,2026 0,1531 0,0769 0,0186
u
2
0,0668 0,1679 0,1453
0
– 0,1171 – 0,1087 – 0,0344
u
3
0,0872 0,1187 – 0,0786 –0,2026 – 0,0634 0,0769 0,0450
u
4
0,0944
0
– 0,2055
0
0,1657
0
- 0.0487
u
5
0,0872 – 0,1187 - 0,0786 0,2026 – 0,0634 – 0,0769 0,0450
u
6
0,0668 – 0,1679 0,1453
0
– 0,1171 0,1087 – 0,0344
u
7
0,0361 – 0,1187 0,1898 – 0,2026 0,1531 – 0,0769 0,0186
На рис. 3 показаны первая и седьмая моды (собственные функции)
для рассмотренной струны. Там же жирными линиями показана форма
колебаний семи характерных участков седьмой моды.
Для формы колебаний характерных участков седьмой моды, ис-
пользуя формулу (12), находим коэффициенты распределения ампли-
туд этой формы по выражению
β
1
−
i
= sin (7
π/
8)
/
sin(7
π/
8)
. Получаем
значения:
β
1
−
1
= 1
,
β
1
−
2
=
−
1
,
8478
,
β
1
−
3
= 2
,
4142
,
β
1
−
4
=
−
2
,
6131
,
β
1
−
5
= 2
,
4142
,
β
1
−
6
=
−
1
,
8478
,
β
1
−
7
= 1
.
Вычислив значения собственных функций
u
i
достаточно большого
числа гармоник и просуммировав их для данных сечений в интер-
вале времени от 0 до
Т
/
2
, найдем прохождение волн по струне и
отклонения ее от первоначального положения. Интересно отметить,
56
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 3


