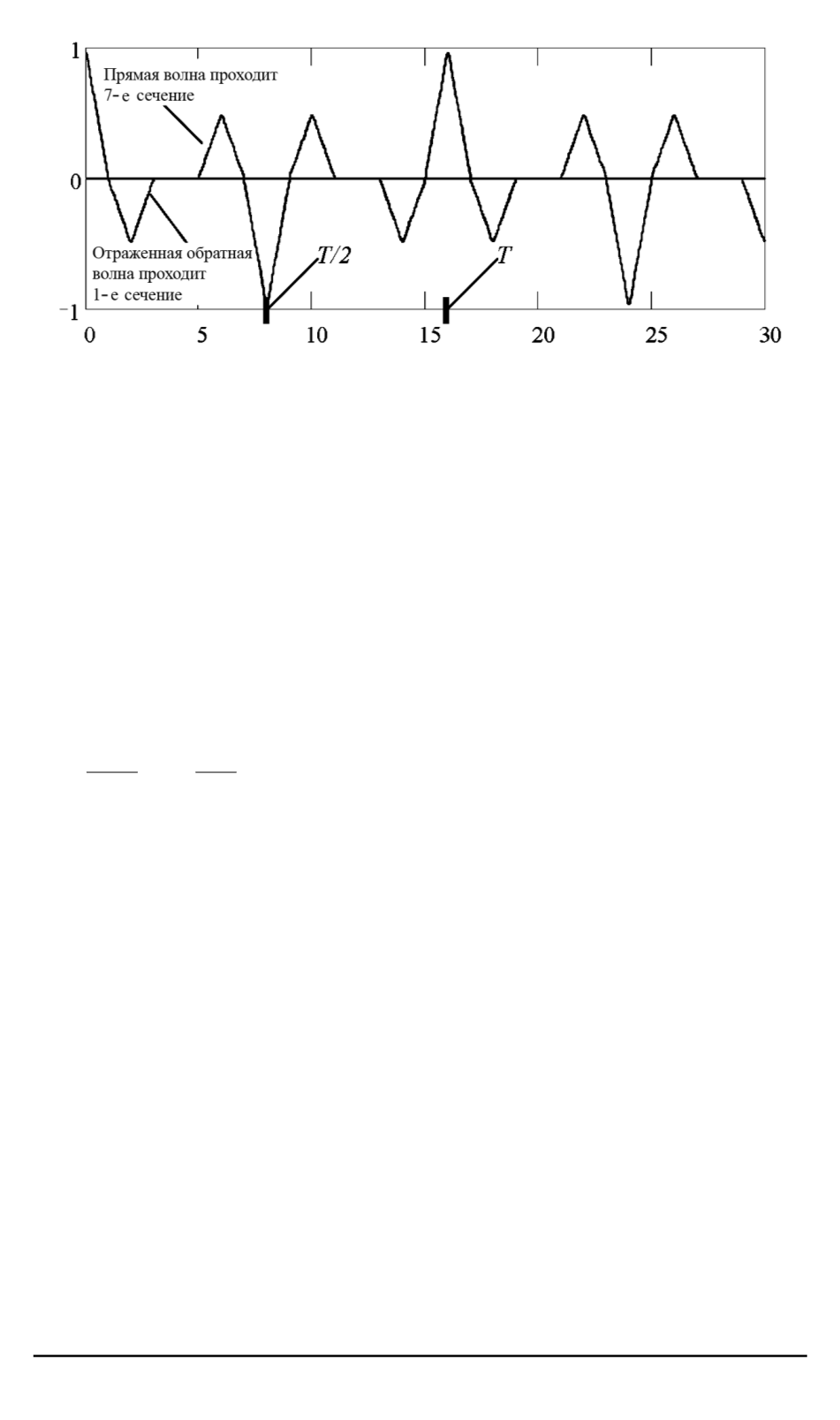
Рис. 4. К прохождению прямой и обратной волнами 1-го и 7-го сечений одно-
родной системы
предполагает для данной математической модели мгновенное распро-
странение механического взаимодействия. К аналогичному результату
приводит и использование уравнения Лагранжа, поскольку потенци-
альная энергия системы является функцией координат взаимодейству-
ющих тел. В этом случае математическая модель различных динамиче-
ских систем (например, крутильной системы) обычно представляется
системой дифференциальных уравнений второго порядка, решение ко-
торой имеет особенности, определяемые бесконечно большой фазовой
скоростью распространения волн:
J
k
d
2
ϕ
k
dt
2
+
ξ
k
dϕ
k
dt
+
m
X
j
=1
c
kj
(
ϕ
k
−
ϕ
j
) =
T
k
(
t
)
, k
= 1
,
2
, . . . , N,
(13)
где
J
k
— момент инерции
k
-й массы;
ϕ
k
,
ϕ
j
— угловые отклонения двух
соседних масс;
ξ
k
— эквивалентный коэффициент внешнего, вязкого
трения для
k
-й массы;
c
kj
— жесткость участка между массами
k
и
j
;
m
— число масс, связанных с
k
-й массой;
Т
k
(
t
)
— возмущающее
воздействие на
k
-ю массу.
Систему дифференциальных уравнений (13) можно решить либо
непосредственно численным интегрированием, либо другими спосо-
бами, например, разложением движения системы по формам собствен-
ных колебаний, методом главных координат, методом комплексных ам-
плитуд, энергетического баланса. Несмотря на то, что для этих методов
расчета исходной является одна и та же система дифференциальных
уравнений, подходы к ee решению различны у разных авторов. Если
одни допускают существование пространственных форм колебаний
[3, 4], получая при решении сдвиги фаз между колебаниями отдель-
ных масс, то другие, использующие метод энергетического баланса,
принимают плоскую форму собственных колебаний [5].
58
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 3


