В начальный момент времени
t
0
= 0
значения
z
10
,
z
20
,
η
0
известны из
начальных условий:
z
10
= 0
,
z
20
= 0
,
η
0
= 0
. Далее для
k
= 0
,
1
,
2
, . . .
проводим вычисления по следующей схеме:
— находим
η
k
+1
по формуле
η
k
+1
=
η
k
+
τ q
(
z
1
k
, z
2
k
, η
k
)
;
— вычисляем
z
1
,k
+1
по формуле
z
1
,k
+1
=
b
(
η
k
+1
)
;
— находим
z
2
,k
+1
как решение уравнения
z
2
=
b
0
(
η
k
+1
)
∙
q
(
z
1
,k
+1
, z
2
, η
k
+1
)
.
Для решения последнего уравнения использовался метод простой
итерации. Расчеты показали, что условие
|
η
N
−
1
|
< δ
выполняется при
N
= 13000
. Таким образом, момент времени
t
≈
t
N
= 1
,
3
. Графики
функций
z
1
(
t
)
,
z
2
(
t
)
,
η
(
t
)
на отрезке
[0
, t
N
]
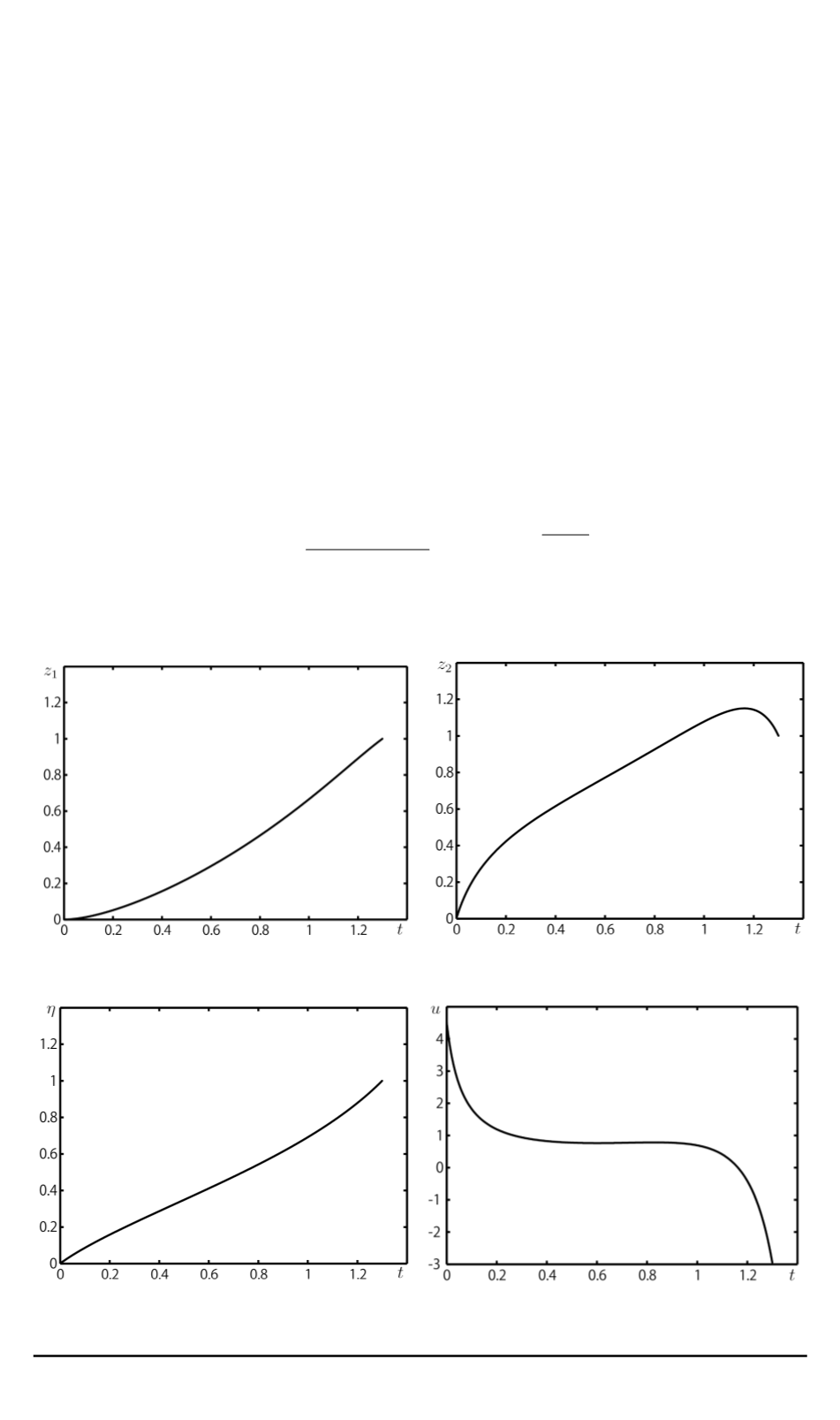
, построенные в результате
работы алгоритма, приведены на рис. 1–3.
Для нахождения значений
u
k
управления
u
в моменты времени
t
k
использовалась формула
u
k
=
z
2
,k
+1
−
z
2
k
τ
,
k
= 0
, N.
График функции
u
(
t
)
приведен на рис. 4.
Рис. 1. График функции
z
1
(
t
)
Рис. 2. График функции
z
2
(
t
)
Рис. 3. График функции
η
(
t
)
Рис. 4. График функции
u
(
t
)
14
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 2


