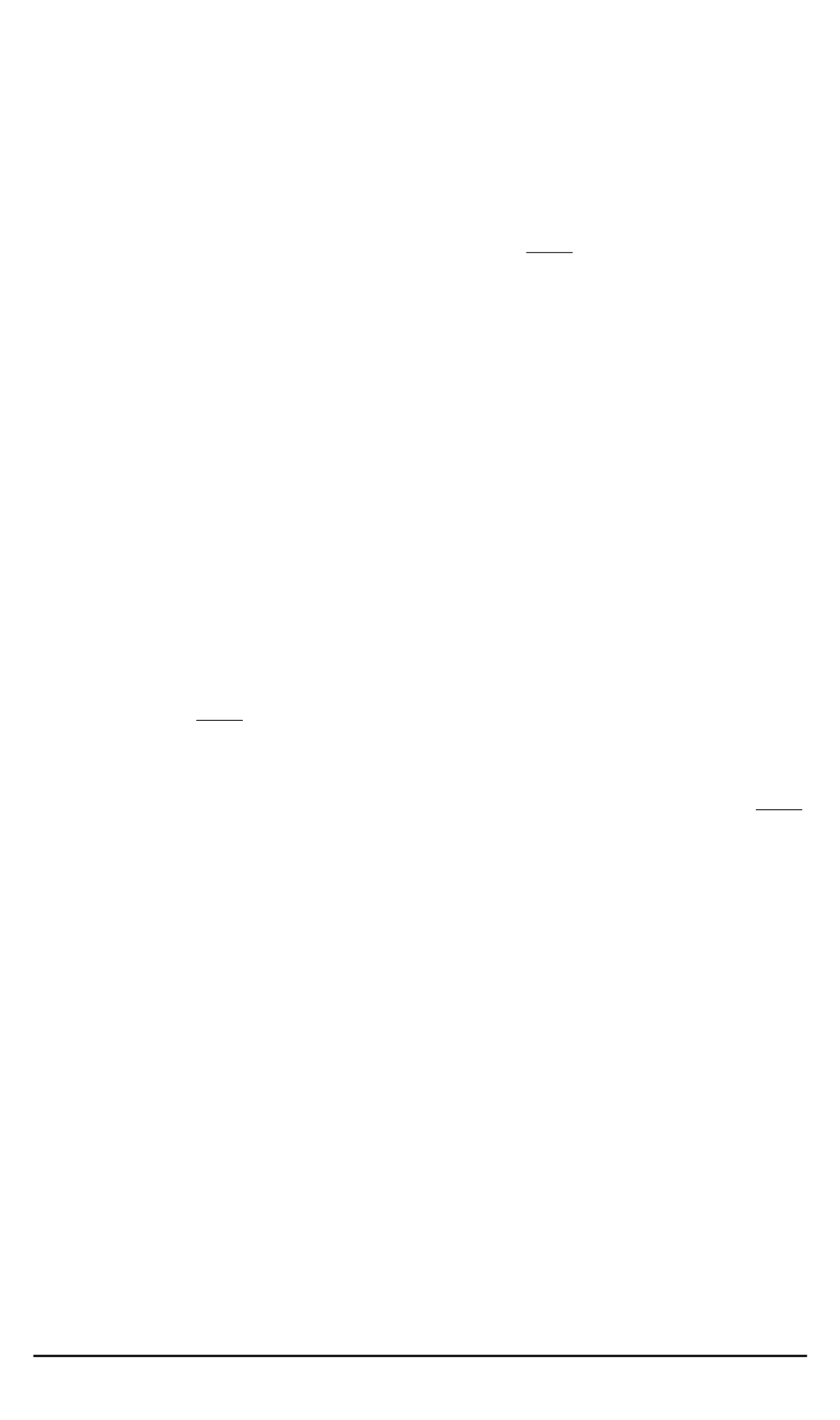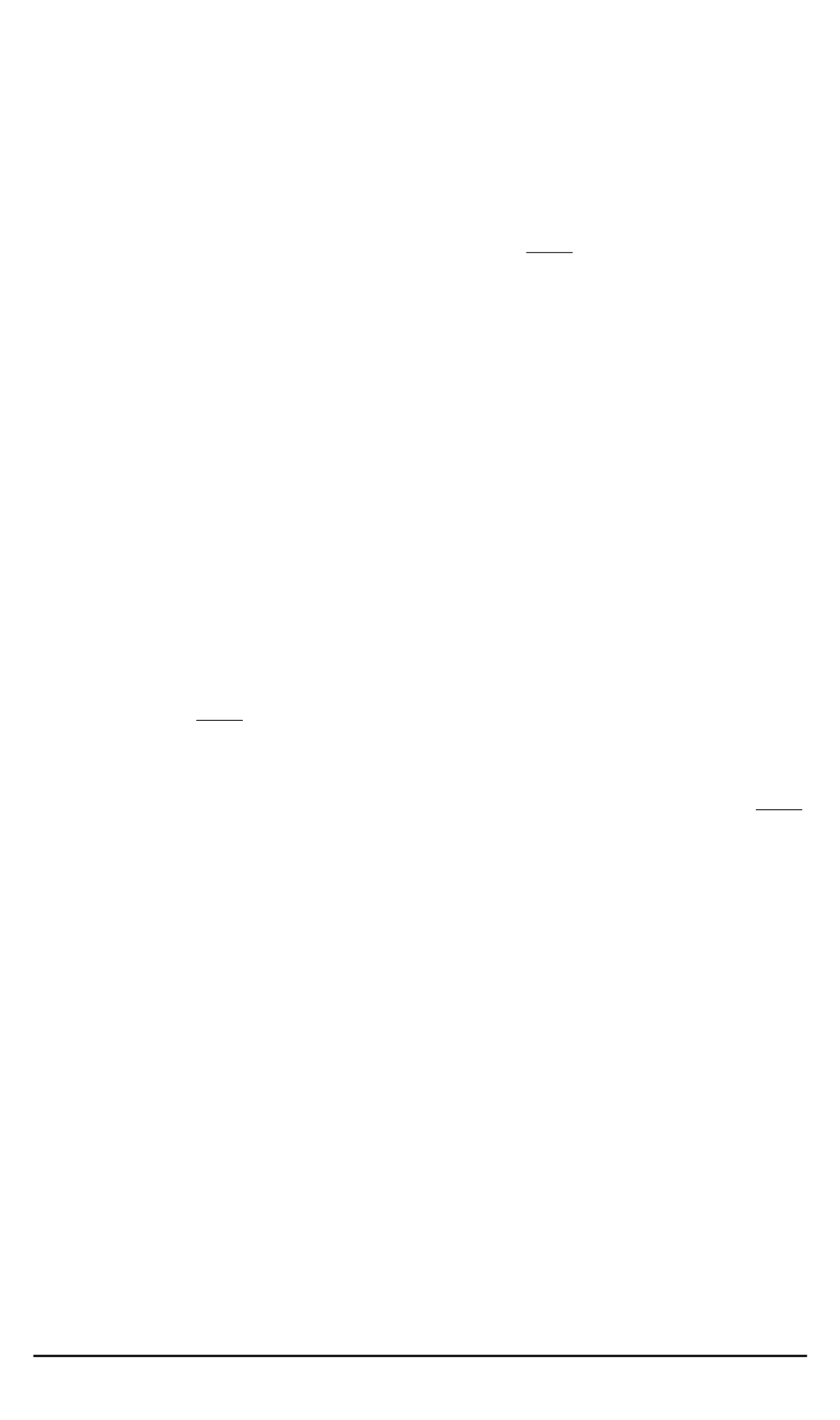
Если система (1) удовлетворяет условиям теоремы 1, то терми-
нальная задача для этой системы преобразуется в терминальную за-
дачу для системы (2) с граничными состояниями
(
z
0
, η
0
) =
ϕ
(
x
0
)
,
(
z , η
) =
ϕ
(
x
)
. Управление
u
(
t
)
, являющееся решением одной из
этих задач, одновременно является решением и другой терминальной
задачи.
Далее будем полагать, что система (1) удовлетворяет условиям те-
оремы 1, причем
ϕ
(Ω) =
R
n
,
r
i
= 2
,
i
= 1
, m
,
ρ
= 1
, система (2)
регулярна: матрица
g
(
z, η
) =
g
11
(
z, η
)
. . . g
1
m
(
z, η
)
...
. . .
...
g
m
1
(
z, η
)
. . . g
mm
(
z, η
)
не вырождена в
R
n
.
3. Решение терминальной задачи для системы квазиканоничес-
кого вида.
При сделанных предположениях система (1) заменой пе-
ременных преобразуется в систему квазиканонического вида
˙
z
i
1
=
z
i
2
,
˙
z
i
2
=
f
i
(
z
1
1
, z
1
2
, . . . , z
m
1
, z
m
2
, η
) +
m
P
j
=1
g
ij
(
z
1
1
, z
1
2
, . . . , z
m
1
, z
m
2
, η
)
u
j
,
˙
η
=
q
(
z
1
1
, z
1
2
, . . . , z
m
1
, z
m
2
, η
)
,
(3)
i
= 1
, m,
(
z
1
1
, z
1
2
, . . . , z
m
1
, z
m
2
)
т
2
R
n
−
1
, η
2
R
,
det
g
(
z, η
)
6
= 0
в
R
n
, q
(
z
1
1
, z
1
2
, . . . , z
m
1
, z
m
2
, η
)
2
C
∞
(
R
n
)
,
f
i
(
z
1
1
, z
1
2
, . . . , z
m
1
, z
m
2
, η
)
, g
ij
(
z
1
1
, z
1
2
, . . . , z
m
1
, z
m
2
, η
)
2
C
∞
(
R
n
)
, i, j
= 1
, m.
Вместо терминальной задачи для системы (1) получаем эквивалент-
ную терминальную задачу для системы (3): для заданного состояния
системы (3) при
t
= 0
z
1
1
(0) =
z
1
10
, z
1
2
(0) =
z
1
20
, . . . , z
m
1
(0) =
z
m
10
, z
m
2
(0) =
z
m
20
, η
(0) =
η
0
(4)
требуется найти такие управления
u
1
=
u
1
(
t
)
, . . . , u
m
=
u
m
(
t
)
, что для
решения
z
1
1
(
t
)
, z
1
2
(
t
)
, . . . , z
m
1
(
t
)
, z
m
2
(
t
)
, η
(
t
)
задачи Коши
˙
z
i
1
=
z
i
2
,
˙
z
i
2
=
f
i
(
z
1
1
, z
1
2
, . . . , z
m
1
, z
m
2
, η
) +
m
P
j
=1
g
ij
(
z
1
1
, z
1
2
, . . . , z
m
1
, z
m
2
, η
)
u
j
(
t
)
˙
η
=
q
(
z
1
1
, z
1
2
, . . . , z
m
1
, z
m
2
, η
)
,
z
1
1
(0) =
z
1
10
, z
1
2
(0) =
z
1
20
, . . . , z
m
1
(0) =
z
m
10
, z
m
2
(0) =
z
m
20
, η
(0) =
η
0
существует момент времени
t
=
t >
0
, в который это решение будет
удовлетворять условиям
6
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 2