Начальные и граничные условия для уравнения концентрации
нефти:
c
нефть
(
r, z,
0) = 1
, r
2
(
R
W
+
H
d
, R
E
)
, z
2
(0
, H
) ;
c
нефть
(
r, z,
0) = 0
, r
2
(
R
W
, R
W
+
H
d
)
, z
2
(0
, H
) ;
c
нефть
(
r, H, t
) = 0
, r
2
(
R
W
, R
W
+
H
d
) ;
c
нефть
(
r, H, t
) = 1
, r
2
(
R
W
+
H
d
, R
E
) ;
c
нефть
(
R
E
, z, t
) = 1
, z
2
(0
, H
) ;
∂c
нефть
(
r,
0
, t
)
∂z
= 0
, r
2
(
R
W
, R
E
) ;
∂c
нефть
(
R
W
, z, t
)
∂r
= 0
, z
2
(0
, H
W
)
.
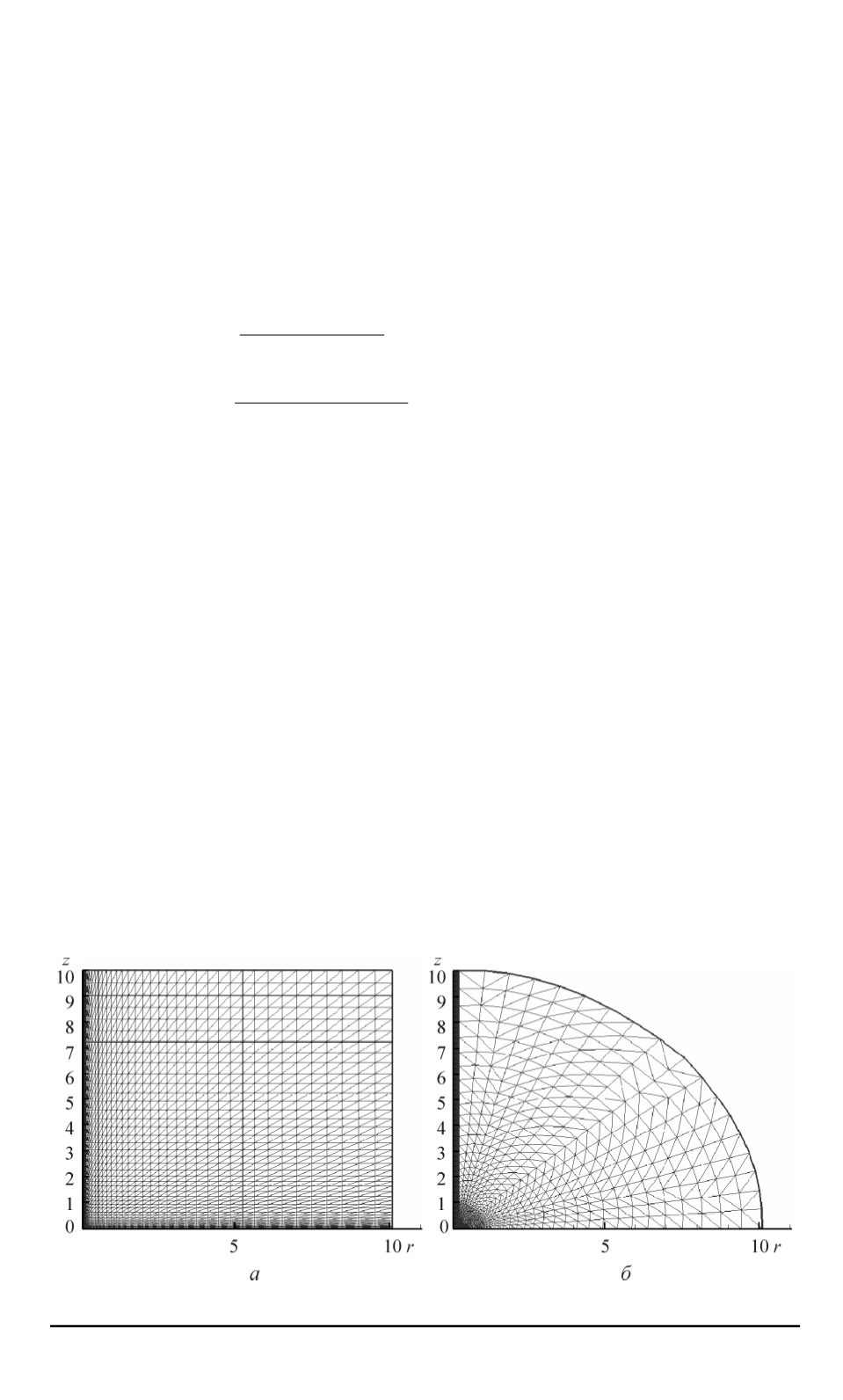
Для демонстрирации эффективности предлагаемого метода задачу
решали на двух сетках. Сравнение результатов проводили с коммер-
ческим программным обеспечением Eclipse-100. Сетка 1 имеет пря-
моугольную топологию и 2601 узел (рис. 3,
a
), она же используется
в Eclipse-100. Сетка 2 имеет сферическую топологию и 1927 узлов
(рис. 3,
б
). Сгущение к поверхности отбора для обеих сеток приведено
на рис. 4.
Среднеинтегральная насыщенность нефти на поверхности отбора
в зависимости от времени приведена на рис. 5. Результаты численного
расчета хорошо согласуются с результатами, полученными с помо-
щью Eclipse-100. Значения расхода нефти через поверхность отбора
следующие:
7
,
78
∙
10
−
2
кг/(м
2
∙
с) (сетка 1);
7
,
69
∙
10
−
2
кг/(м
2
∙
с) (сетка 2);
7
,
16
∙
10
−
2
кг/(м
2
∙
с) (Eclipse-100).
Выводы
. Разработан вариант МКЭКО с равным порядком интер-
поляции скорости и давления для решения задач однофазной филь-
трации. Оценка метода проводилась с помощью ряда тестовых задач:
Рис. 3. Сетка 1 (
а
) и сетка 2 (
б
) расчетной области
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 4
85


