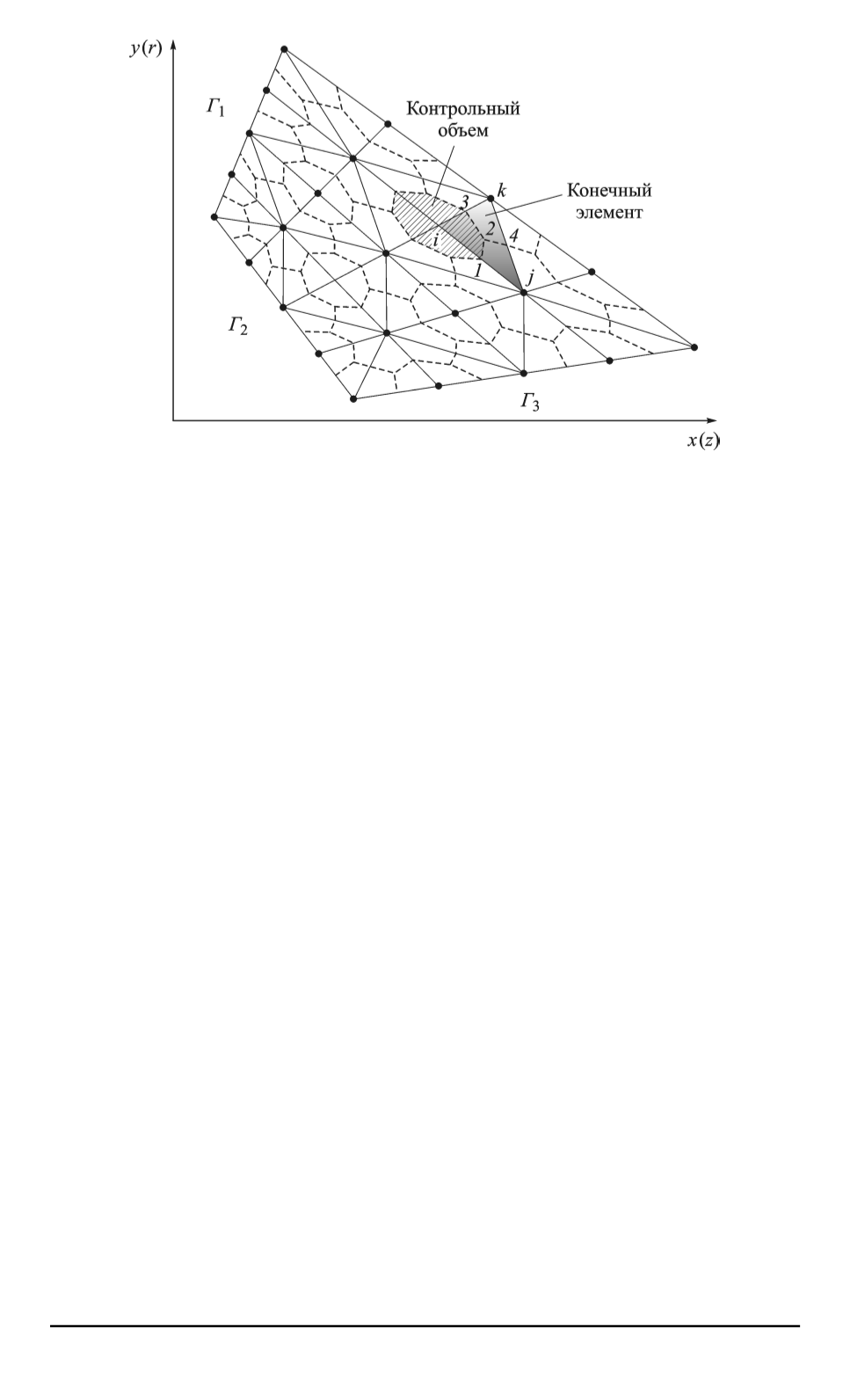
Рис. 1. Разбиение расчетной области
узел, в одну область, которая будет называться контрольным объемом
для данного узла.
Контрольный объем
для узла
i
выделен штриховкой
на рис. 1. Полученные таким образом контрольные объемы обладают
следующими отличителными свойствами: они не перекрываются, пол-
ностью заполняя расчетную область; их границы не включают меж-
элементных границ; они могут быть построены на любой треугольной
сетке, включающей и тупоугольные треугольники.
Интерполяция на элементе.
На элементе
i–j–k
могут применяться
два вида интерполяции — линейная и ступенчатая. Линейная интер-
поляция:
Φ =
N
i
Φ
i
+
N
j
Φ
j
+
N
k
Φ
k
, где
[
N
] = [
N
i
N
j
N
k
]
— функ-
ции формы, которые для треугольного линейного элемента имеют вид,
представленный в [1]. Если на элементе используется ступенчатая ин-
терполяция, то считается, что значение функции
Φ
постоянно по всему
контрольному объему для данного узла и равно значению функции в
узле.
Случай анизотропного пласта.
В метод включен общий случай
анизотропии пласта. Главные оси проницаемости
(
x
0
, y
0
)
и теплопро-
водности
(
x
00
, y
00
)
на элементе повернуты относительно глобальных
осей координат
(
x, y
)
на углы
χ
и
θ
соответственно. Для удобства
будем использовать локальные системы координат
(
X
0
, Y
0
)
,
(
X
00
, Y
00
)
,
оси которых совпадают с главными осями проницаемости и тепло-
проводности соответственно, а начало координат совпадает с началом
глобальной системы координат. Тогда тензоры [
β
], [
K
] в системах
координат
(
x, y
)
,
(
x
0
, y
0
)
,
(
X
0
, Y
0
)
принимают вид
[
β
] =
β
xx
β
xy
β
yx
β
yy
=
β
x
0
0
0
β
y
0
=
β
X
0
0
0
β
Y
0
;
76
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 4


