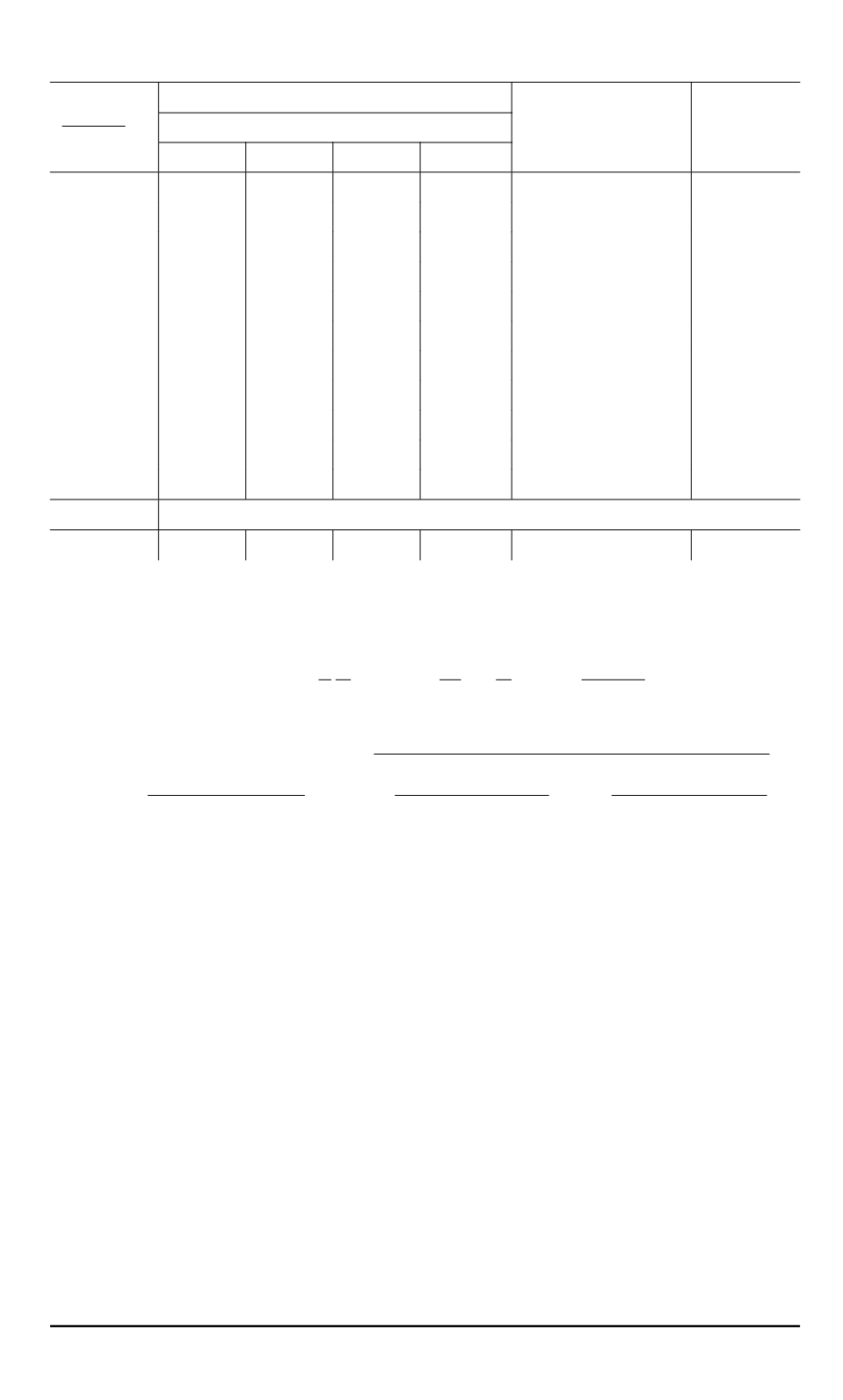
Таблица 2
r
−
r
1
r
2
−
r
1
Давление, MПа (численное решение) Давление,
MПа
(точное решение)
Погреш-
ность, %
Сетка
11
×
11 21
×
21 41
×
41 61
×
61
1,0
1,000 1,000 1,000 1,000
1,000
0
0,9
3,207 3,137 3,023 3,008
2,976
7,76–1,08
0,8
4,373 4,237 4,169 4,156
4,133
5,81–0,56
0,7
5,265 5,137 5,094 5,085
5,069
3,87–0,32
0,6
6,045 5,938 5,910 5,905
5,893
2,58–0,20
0,5
6,766 6,679 6,661 6,658
6,649
1,76–0,14
0,4
7,449 7,380 7,369 7,368
7,361
1,20–0,10
0,3
8,107 8,054 8,049 8,049
8,044
0,78–0,06
0,2
8,749 8,711 8,710 8,710
8,707
0,48–0,03
0,1
9,380 9,358 9,359 9,359
9,357
0,25–0,02
0,0
10,000 10,000 10,000 10,000
10,000
0
Расход воздуха
G
, кг/(м
2
∙
с)
4,592 4,785 4,776 4,735
4,703
2,36. . . 0,68
Имеем выражения для давления
P
=
P
2
1
=
1
2
μ
k
GRT
ln
r
r
1
−
β
8
G
2
RT
r
−
r
1
rr
1
и расхода воздуха
G
=
−
2
μr
2
r
ln(
r
2
/r
1
)
βk
(
r
2
−
r
1
)
+ 4
s
μr
2
r
1
ln(
r
2
/r
1
)
2
βk
(
r
2
−
r
1
)
2
+
r
2
r
1
(
P
2
1
−
P
2
2
)
2
βRT
(
r
2
−
r
1
)
.
Численное решение проводим на сетках c числом узлов
11
×
11
,
21
×
21
,
41
×
41
,
61
×
61
расчетной области. Результаты хорошо согласу-
ются с аналитическим решением (табл. 2).
Задача пробоотбора.
После процесса бурения скважины радиусом
R
w
= 0
,
1
м пласт радиусом
R
e
= 3
,
1
м и высотой
H
= 10
м заполнен
буровым раствором на глубину
H
d
= 0
,
1
м. Пласт имеет пористость
φ
= 0
,
3
и проницаемость
k
= 0
,
5
∙
10
−
12
м
2
. Нефть отбирается через
поверхность отбора высотой
H
w
= 0
,
01125
м, куда попадает вместе
с буровым раствором под действием перепада давлений (пластовое
давление
P
e
= 20
MПа, давление на забое
P
w
= 15
MПа). Свой-
ства нефти и бурового раствора считаются одинаковыми: вязкость
μ
нефть
=
μ
бур.раств
=
μ
= 0
,
01
Па
∙
с,
ρ
нефть
=
ρ
бур.раств
=
ρ
= 1000
кг/м
3
.
Фазовые проницаемости предполагаются линейными функциями на-
сыщенности
k
нефть
=
S
нефть
,
k
бур.раств
=
S
бур.раств
. Необходимо опреде-
лить расход нефти через поверхность отбора и среднеинтегральную
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 4
83


