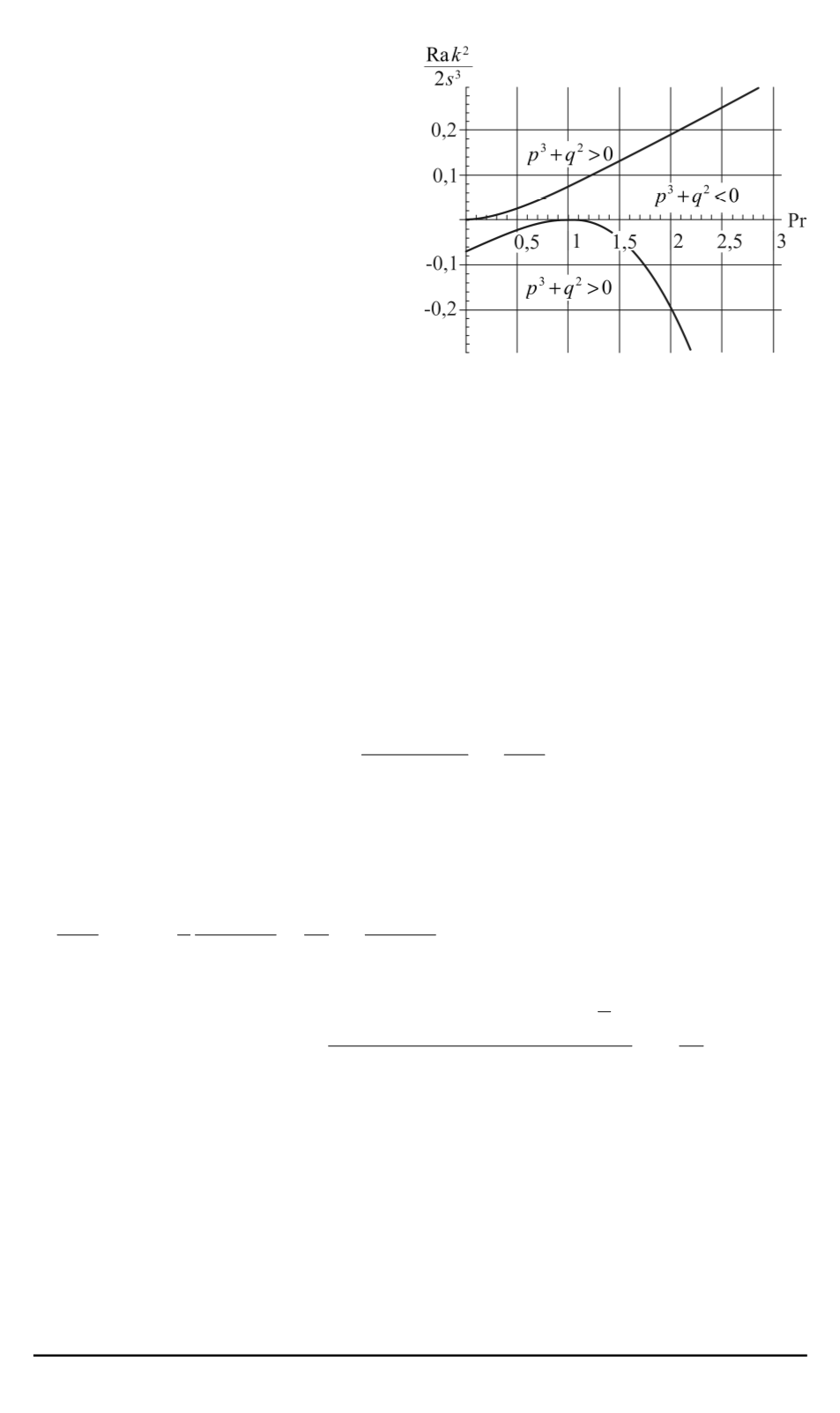
Рис. 3. Кривые вырождения и области
чисто мнимых, действительных и ком-
плексных решений
Кривые (11) — по сути би-
фуркационные, а рис. 3 — это
бифуркационная диаграмма для
множества функций профиля,
так как эти кривые определяют
множества значений комплек-
сов параметров волн, при кото-
рых появляется пара осцилли-
рующих решений вместо одного
монотонного.
Следует подчеркнуть, что
явление бифуркации в задаче о
распространении волн, которое
выражалось в появлении допол-
нительных решений в линейной
теории, встречалось и ранее [3, 4]. В работе [3] впервые были найдены
бифуркационные ветвления решений в задаче о волнах на поверхно-
сти вязкой жидкости в отсутствие электрического поля, а в работе [4]
впервые решалась аналогичная задача с учетом действия пондеромо-
торных сил, возникающих в вертикальном электрическом поле.
Если действительные значения принимает первая пара решений
ζ
2
1
,
тогда решения уравнения
ζ
2
1
=
k
2
−
s
(
Pr
+ 1)
3
+
2
p
q
1/3
= 0
определяют границу между положительными и отрицательными реше-
ниями. После элементарных алгебраических преобразований имеем
Ra
2
k
4
=
9
2
Pr
+ 1
Pr
3
+ 1
k
2
s
−
Pr
+ 1
3
−
3
−
−
(
Pr
+ 1) (
Pr
−
2)
Pr
−
1
2
27
s
k
2
3
.
(12)
Поверхность, определяемая уравнением (12), приведена на pиc. 4.
Для точек, расположенных ниже поверхности (12), решение положи-
тельно, что соответствует монотонным функциям профиля, точки над
поверхностью (12) определяют функции профиля в синусоидальном
виде. При этом действительная часть пары комплексно-сопряженных
решений будет иметь соответственно положительное значение над по-
верхностью и отрицательное — под поверхностью.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 3
25


