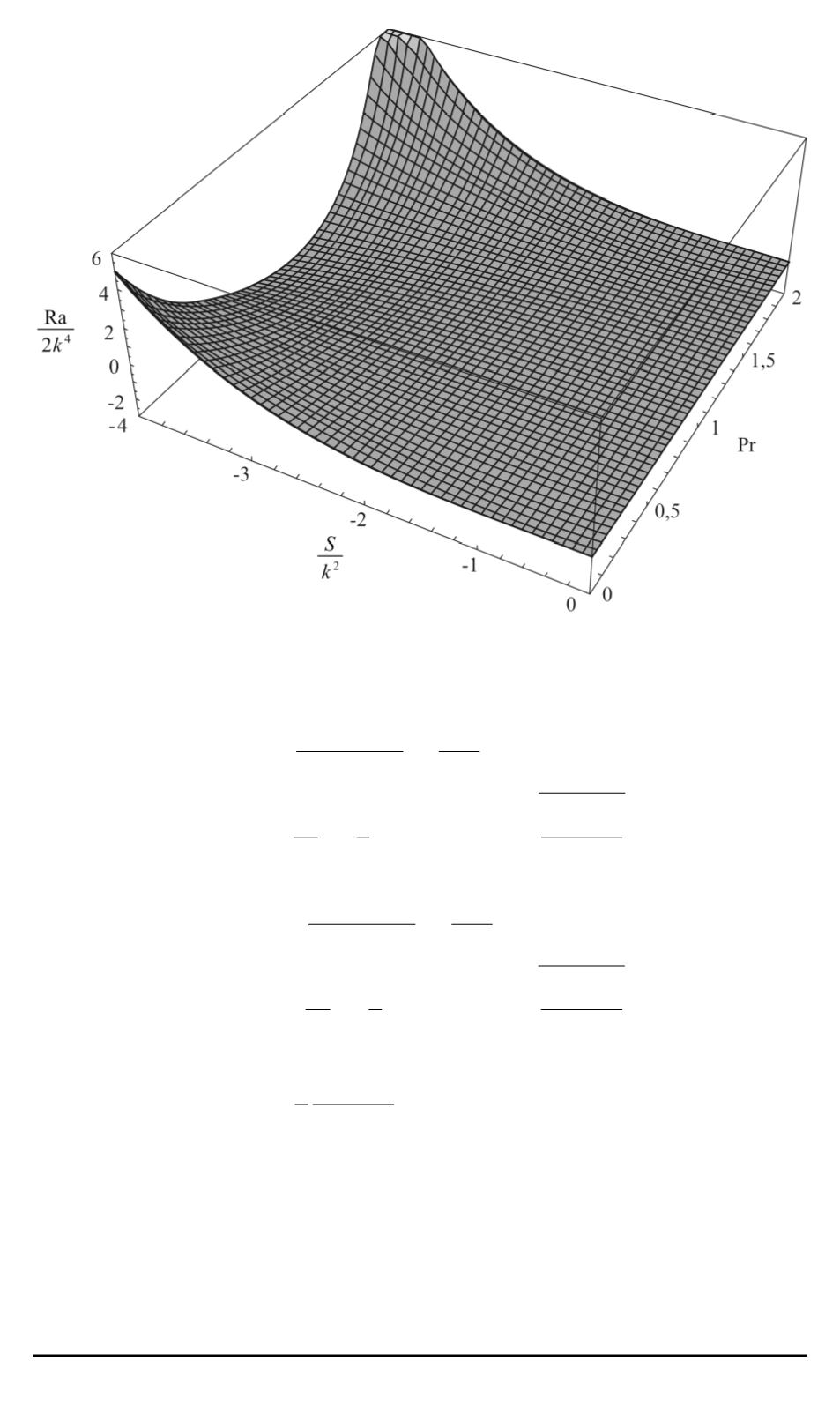
Рис. 4. Поверхность
ζ
2
1
= 0
В случае, когда все решения действительные, можно получить
ζ
2
1
=
k
2
−
s
(
Pr
+ 1)
3
+
2
p
q
1/3
;
ζ
2
1
= 0
,
k
2
s
=
1
3
Pr
+ 1
±
2
s
Pr
3
+ 1
Pr
+ 1
;
ζ
2
2;3
=
k
2
−
s
(
Pr
+ 1)
3
−
p
q
1/3
;
ζ
2
2;3
= 0
,
k
2
s
=
1
3
Pr
+ 1
±
s
Pr
3
+ 1
Pr
+ 1
;
q
=
±
s
3
1
9
Pr
3
+ 1
Pr
+ 1
3/2
.
(13)
На pиc. 5 приведены кривые, определяемые формулами (13) при
равенстве значений
ζ
2
нулю, обозначены области положительных и
отрицательных значений
ζ
2
. Ответить на вопрос, каким волнам со-
ответствует определенный амплитудный профиль по глубине, мож-
но имея дисперсионное соотношение, а также зная значение числа
Прандтля.
26
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 3


