линейных алгебраических уравнений
ζ
j
A
j
= 0;
X
j
A
j
= 0;
A
j
ζ
2
j
−
k
2
= 0;
ζ
2
j
+
k
2
A
j
exp [
ζ
j
] = 0;
A
j
exp [
ζ
j
] = 0;
μζ
j
ζ
2
j
−
3
k
2
+
k
2
1
−
F
√
W
k
+
k
2
W
ζ
2
j
−
k
2
A
j
exp [
ζ
j
] = 0;
ζ
1
,
2
=
k
2
−
Ra
1/3
k
2/3
;
ζ
2
3
,
4
,
5
,
6
=
k
2
+
1
2
1
±
i
√
3
Ra
1/3
k
2/3
,
j
= 1
. . .
6
.
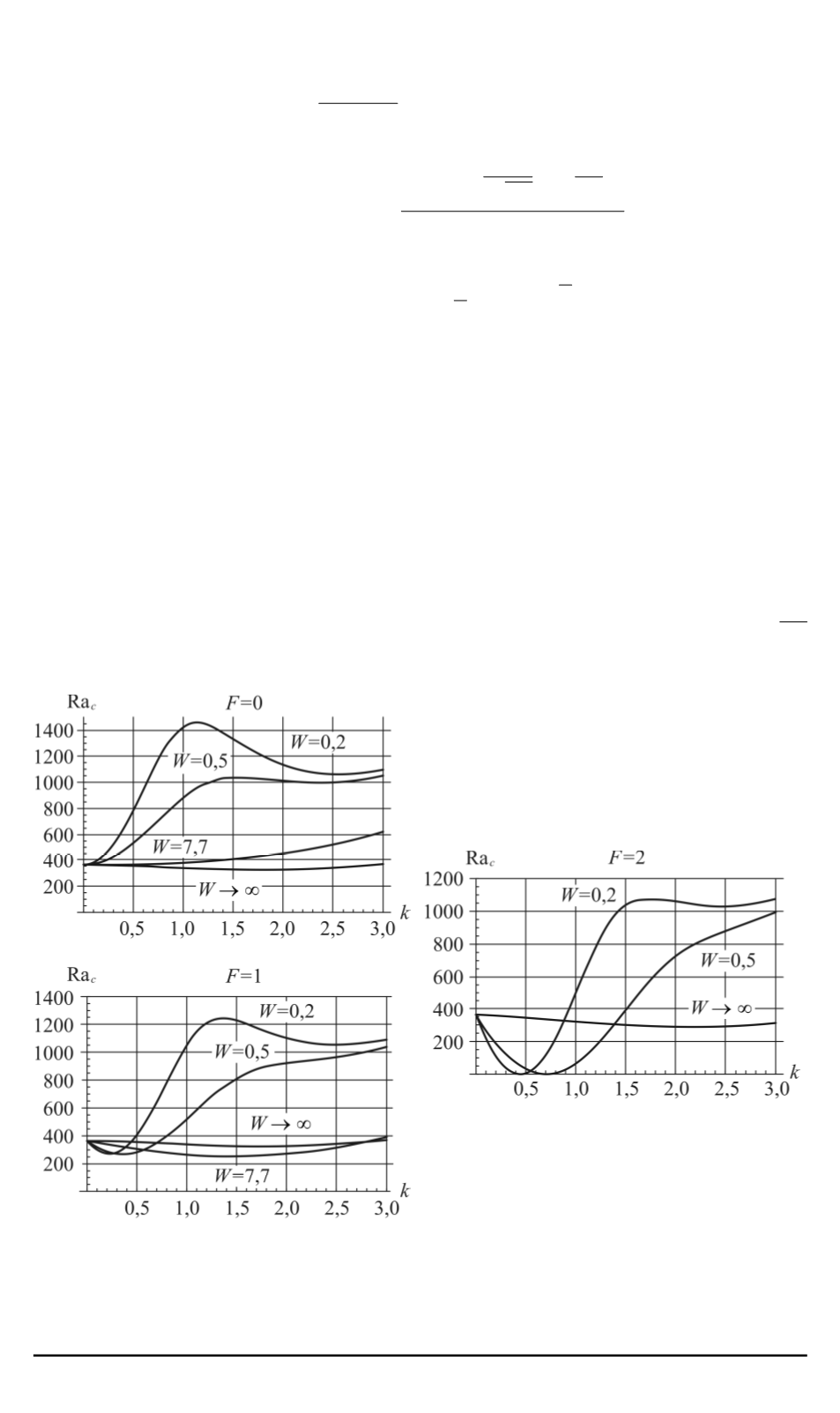
Классическая неустойчивость Френкеля–Тонкса наступает при зна-
чении параметра
F
= 2
.
На pиc. 1 и 2 приведены кривые зависимости критического числа
Рэлея от волнового числа для случая отсутствия электрического поля,
что совпадает с рассмотренным в работе [2], а также в случае докри-
тического и критического поля с параметрами
F
= 1
и
F
= 2
. Из про-
веденного численного расчета следует, что электрическое поле снижа-
ет значения критических чисел Рэлея. При достижении критического
значения напряженности электрического поля на волнах с
k
=
√
W
Рис. 1. Графики критических значе-
ний чисел Рэлея в отсутствие поля
(
F
= 0
) и в случае докритического по-
ля (
F
= 1
)
Рис. 2. Графики критических чисел
Рэлея в случае критического поля
(
F
= 2
)
22
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 3


