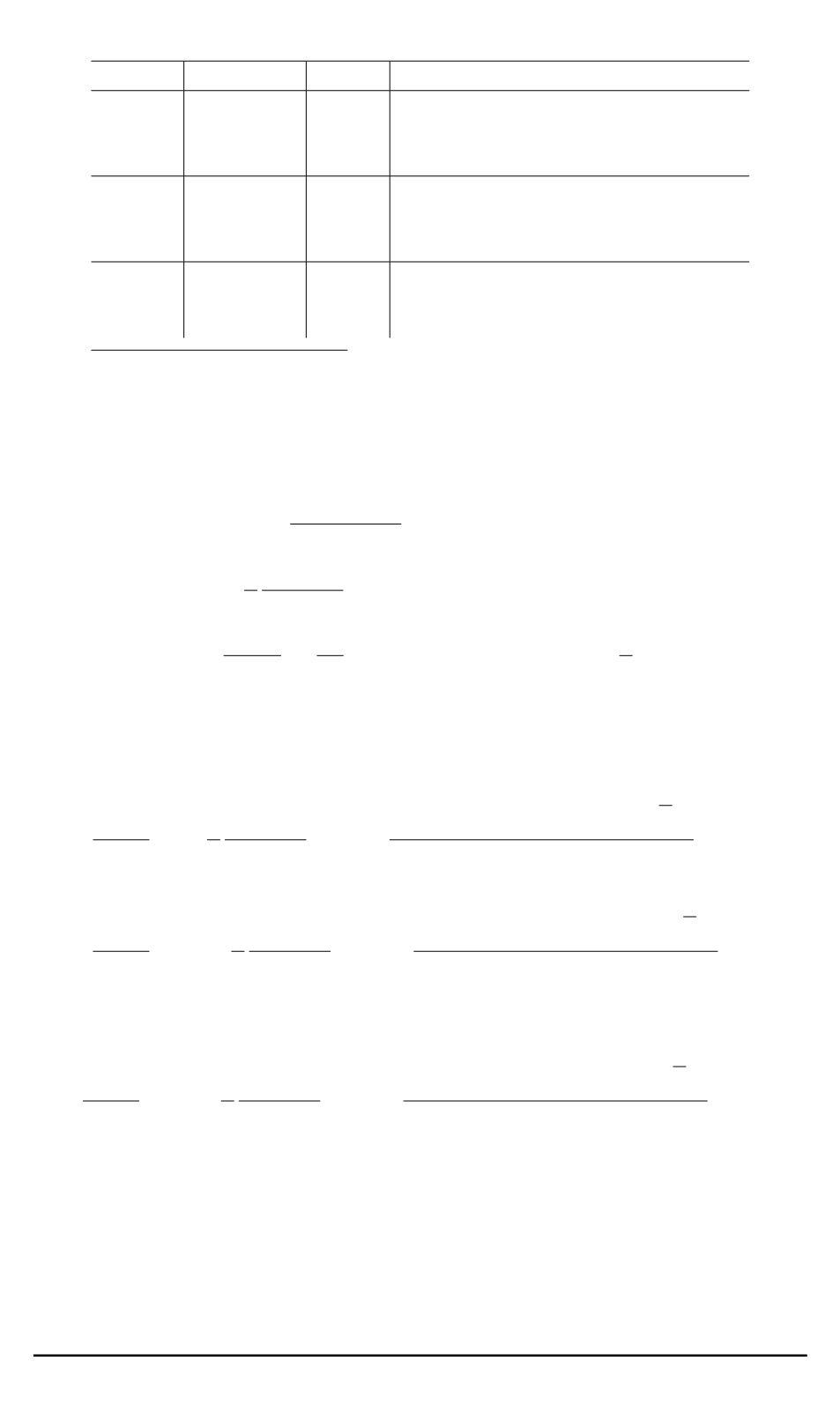
Таблица
ζ
2
s
=
iω
y
i
Вид амплитудной функции
ζ
2
>
0
s
2
R
,
s <
0
,
Ra
>
0
,
y >
0
Монотонная,
экспоненциально
затухающая или возрастающая
по глубине
ζ
2
<
0
s
2
R
,
s >
0
,
Ra
<
0
,
y <
0
Синусоидальная, не затухающая
по глубине
ζ
2
2
C
s
2
C
,
Ra
<
0
y
2
C
Немонотонная, экспоненциально
затухающая или возрастающая
по амплитуде синусоида
П р и м е ч а н и е.
R
— множество действительных чисел;
C
— множество
комплексных чисел.
Перепишем выражения (6) с использованием
s
-параметра
ζ
2
i
=
k
2
−
s
(
Pr
+ 1)
3
+
x
i
, i
= 1
,
2
,
3;
p
=
−
1
9
Pr
3
+ 1
Pr
+ 1
s
2
;
q
=
Ra
k
2
2
+
s
3
27
(
Pr
+ 1) (
Pr
−
2)
Pr
−
1
2
.
(9)
Действительное значение первого корня достигается при
p
3
+
+
q
2
>
0
, что равносильно двум неравенствам:
Ra k
2
2
s
3
>
1
9
Pr
3
+ 1
Pr
+ 1
3/2
−
(
Pr
+ 1) (
Pr
−
2)
Pr
−
1
2
27
;
Ra k
2
2
s
3
6
−
1
9
Pr
3
+ 1
Pr
+ 1
3/2
−
(
Pr
+ 1) (
Pr
−
2)
Pr
−
1
2
27
.
(10)
Второй и третий корни действительны при
Ra k
2
2
s
3
=
±
1
9
Pr
3
+ 1
Pr
+ 1
3/2
−
(
Pr
+ 1) (
Pr
−
2)
Pr
−
1
2
27
.
(11)
Пара кривых (11) приведена на pиc. 3. В точках, принадлежащих
области
p
3
+
q
2
<
0
, все три решения комплексные; кривые соот-
ветствуют случаю трех действительных корней, причем два из них
совпадают, т.е. имеет место вырождение шести линейно независимых
амплитудных функций в четыре. Остальные точки отвечают случаю
одного действительного и двух комплексно-сопряженных корней.
24
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 3


