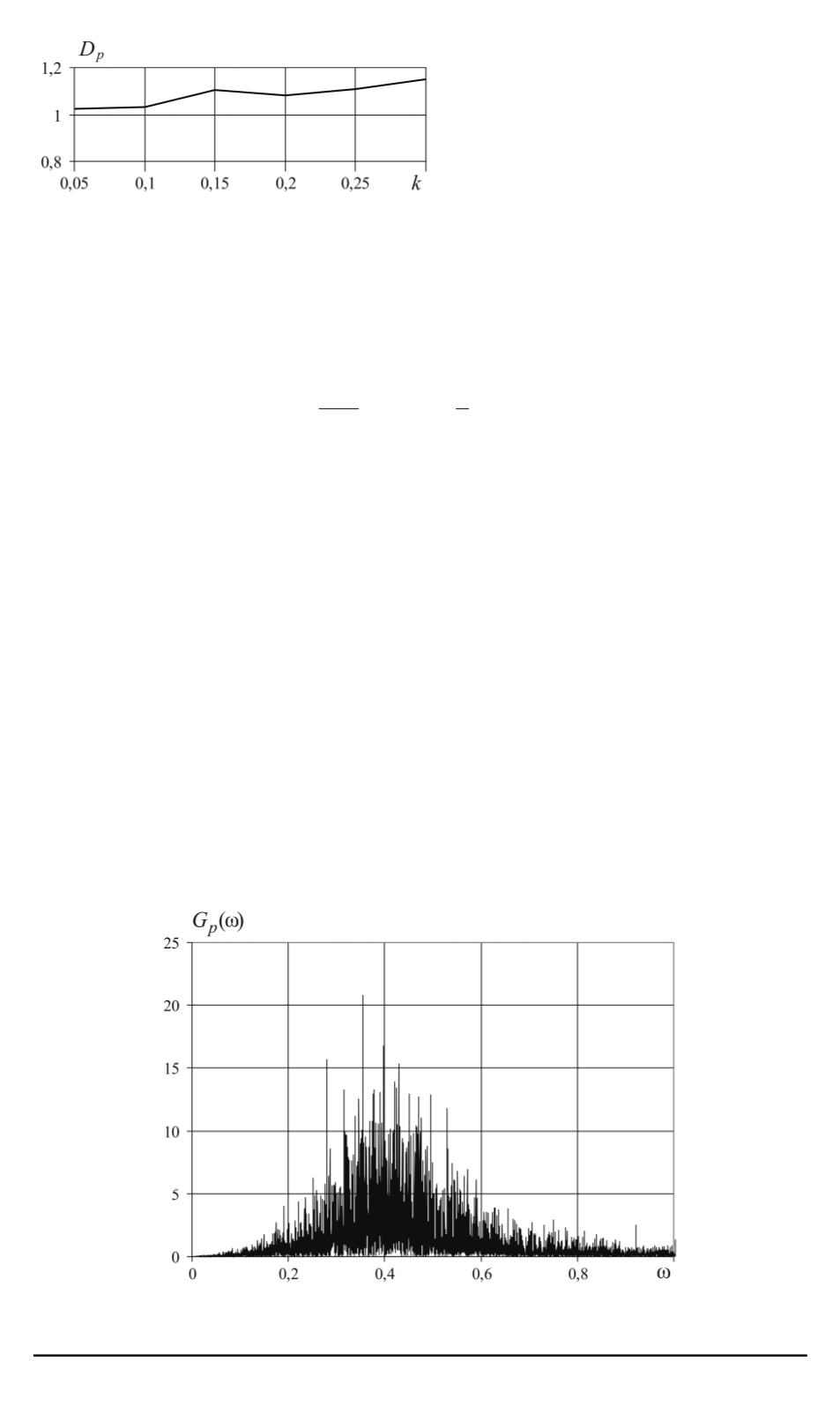
Рис. 5. Зависимость дисперсии флуктуа-
ций импульса
D
p
от коэффициента упру-
гости
k
при
F
= 0
пропорциональной зависимо-
сти, что подтверждается резуль-
татами численного расчета (см.
формулу (30)).
Дисперсия флуктуаций им-
пульса осциллятора
D
p
почти не
меняется с ростом коэффициен-
та упругости
k
(соответствую-
щая зависимость приведена на
рис. 5) и принимает значение, близкое к единице. Это также согласу-
ется с классической моделью. Действительно, так как
1
2
M
P
2
=
1
2
k
B
T,
(34)
а дисперсия импульса определяется выражением
D
p
=
P
2
,
(35)
находим
D
p
=
Mk
B
T,
(36)
т.е. дисперсия флуктуаций импульса зависит только от массы осцил-
лятора и температуры среды и не зависит от коэффициента упруго-
сти. Незначительный рост дисперсии флуктуаций импульса осцилля-
тора
D
p
с увеличением параметра упругости
k
(см. рис. 5) связан,
по-видимому, с возрастанием ошибок численного моделирования при
увеличении собственной частоты колебаний осциллятора.
На рис. 6 представлены результаты численного расчета спектраль-
ной плотности флуктуаций импульса
P
при
k
= 0
,
1
и
F
= 0
. Видно,
что представленный график носит характер резонансной кривой.
Рис. 6. Характерный вид спектральной плотности флуктуации импульса
G
p
при
k
= 0
,
1
и силе
F
= 0
12
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2


