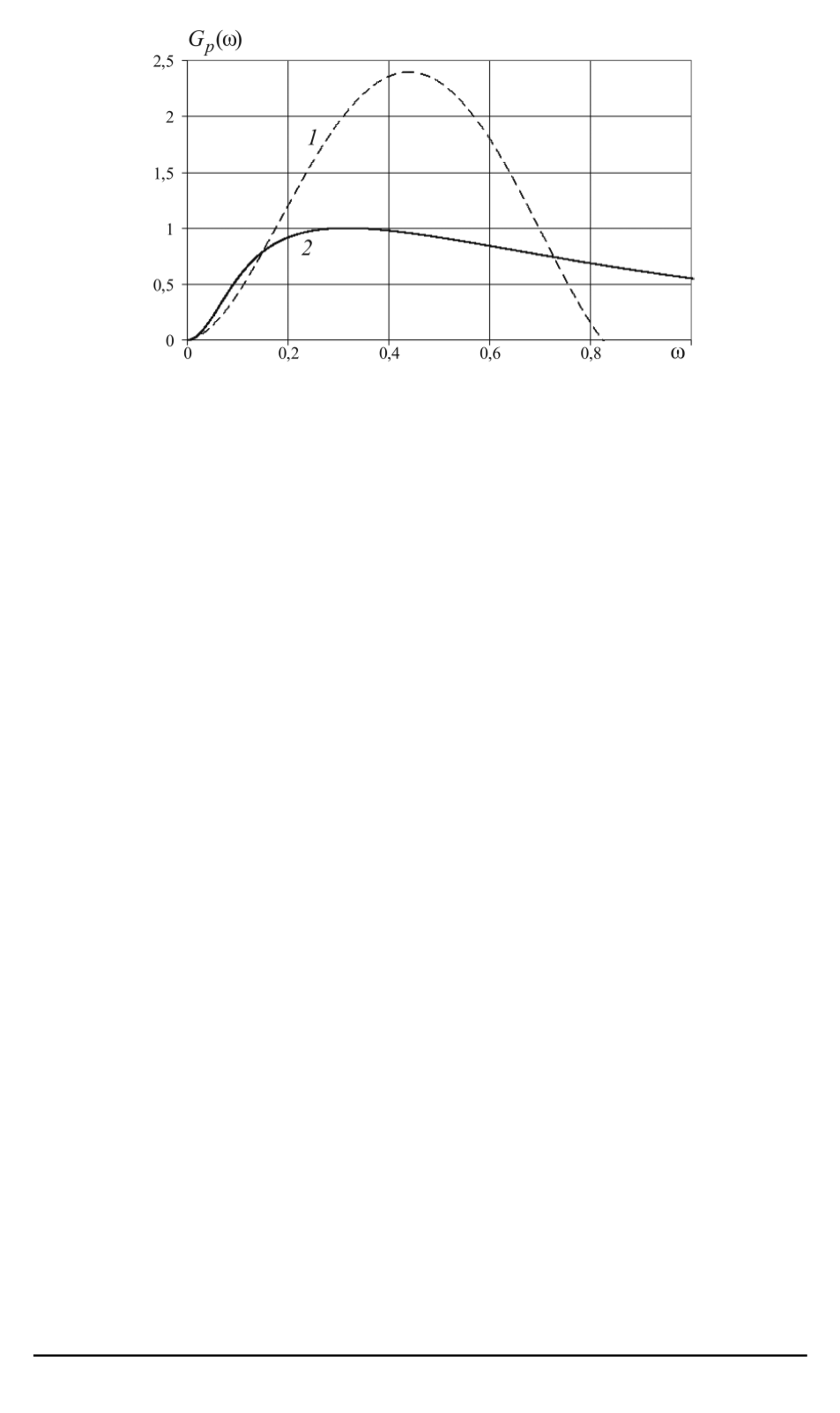
Рис. 9. Резонансные кривые для осциллятора, находящегося под воздействием
флуктуирующего коэффициента трения (
1
), и классического осциллятора (
2
)
жении (38) близок к 1, что является следствием того, что при расчетах
принято
M
= 1
.
На рис. 9 представлены резонансные кривые для классического ос-
циллятора и осциллятора, описываемого выражением (28). В обоих
случаях принято, что параметр упругости
k
= 0
,
1
. Для неклассиче-
ского осциллятора резонансная кривая получена путем аппроксима-
ции численных результатов полиномом четвертой степени. Видно, что
кривая, соответствующая неклассическому случаю, в области средних
частот заметно выше резонансной кривой, соответствующей класси-
ческой теории, а резонансная частота в первом случае несколько боль-
ше. Отметим, что суммарная площадь под кривыми в обоих случаях
близка к единице.
Выводы.
Использование вместо классического дифференциаль-
ного уравнения Ланжевена интегрального уравнения (12) позволя-
ет учесть экспериментально наблюдаемые флуктуации коэффициен-
та трения типа фликкер-шума. Посредством этого уравнения описано
движение броуновской частицы, находящейся в среде с флуктуирую-
щим коэффициентом трения, что является более точным по сравнению
с классическим описанием.
Применение рассмотренной модели к случаю осциллятора пока-
зывает, что полученные для осциллятора зависимости согласуются с
аналогичными для классической модели, но являются более точными,
так как учитывают флуктуирующий характер коэффициента трения.
Полученные результаты могут найти применение в различных за-
дачах, использующих модели броуновского движения и осциллятора,
в том случае, если параметр, характеризующий “сопротивление” опи-
сываемой физической или технической системы, испытывает флукту-
ации, имеющие вид фликкер-шума.
14
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2


