постоянная величина (
σ
ξ
=
D
), окончательно получим
G
p
(
ω
) =
ω
2
ω
4
+ (
η
2
−
2
ω
2
0
)
ω
2
+
ω
4
0
D.
(27)
Броуновская частица как осциллятор в среде с флуктуирую-
щим коэффициентом трения.
Если осциллятор находится в среде с
флуктуирующим коэффициентом трения, то вместо дифференциаль-
ного уравнения Ланжевена (23) для его описания применимо уравне-
ние
˙
P
+
t
Z
0
W
(
t
−
τ
)
t
−
τ
dW
(
τ
)
dτ
P
(
τ
)
Mk
B
T
dτ
=
−
kY
(
t
) +
F
(
t
) +
ξ
(
t
)
.
(28)
Уравнения (28) решается численно. При вычислениях шаг по вре-
мени принят
Δ
t
= 0
,
3
, произведение
Mk
B
T
= 1
,
M
= 1
, интенсив-
ность белого шума
ν
= 1
. Внешняя сила варьировалась в диапазоне
F
= 0
,
0
. . .
1
,
0
с шагом
Δ
F
= 0
,
1
. Параметр
k
принят равным
0
,
1
. Кро-
ме того, расчеты проводили при заданных значениях внешней силы
(
F
= 0
,
0
и
F
= 0
,
5
) и разных значениях
k
в диапазоне
k
= 0
,
05
. . .
0
,
3
с шагом
Δ
k
= 0
,
05
. Все величины формально считали безразмерны-
ми. В каждом случае получено 10
5
значений импульса и координаты
осциллятора.
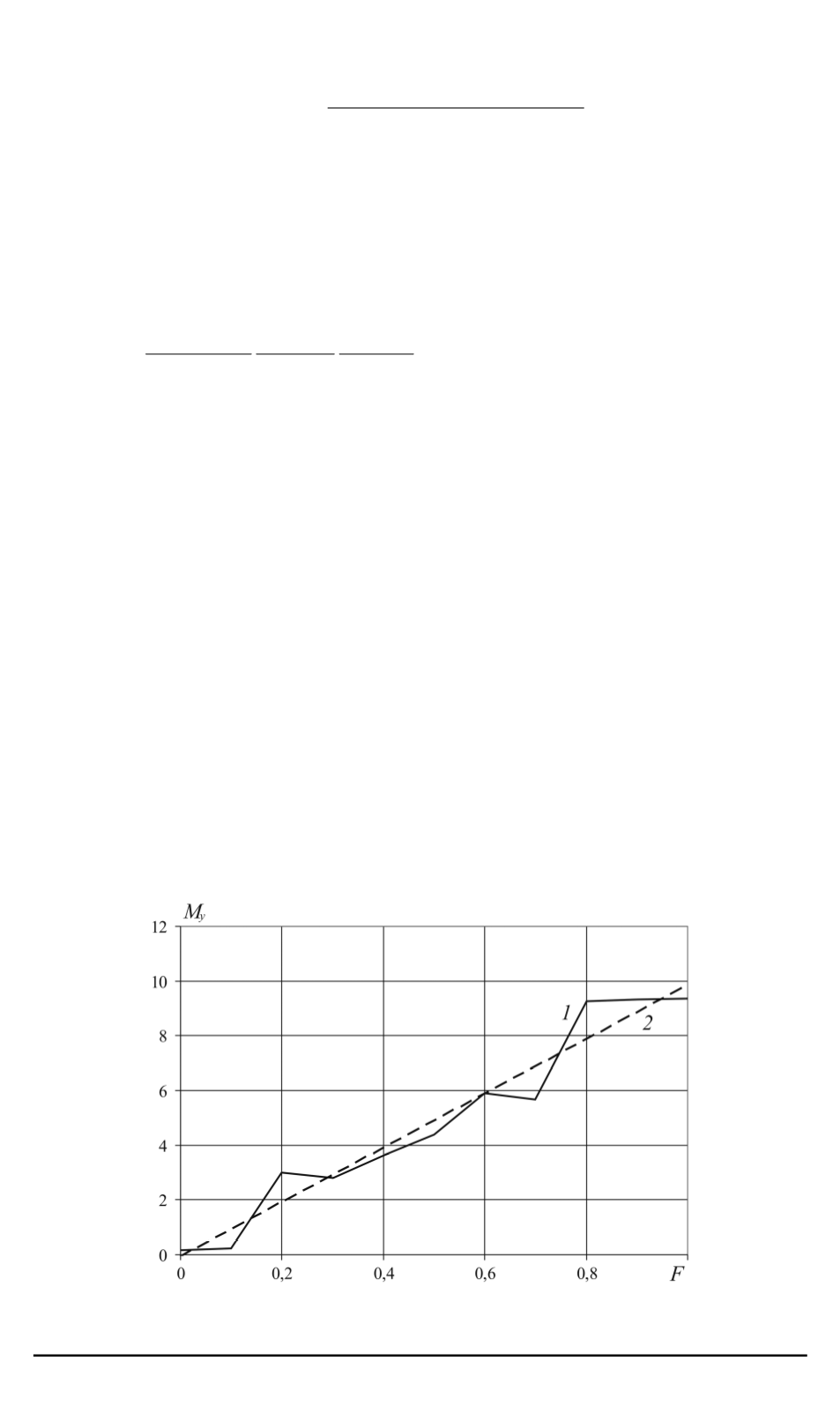
На рис. 3 показана зависимость математического ожидания коорди-
наты частицы
M
y
от приложенной силы, которая, как видно, является
линейной. Уравнение прямой, построенной при аппроксимации мето-
дом наименьших квадратов, имеет вид
M
y
= 9
,
932
F
−
0
,
081
.
(29)
Рис. 3. Зависимость математического ожидания координаты частицы
M
y
от
приложенной внешней силы
F
(
1
) и прямая аппроксимации (
2
)
10
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2


