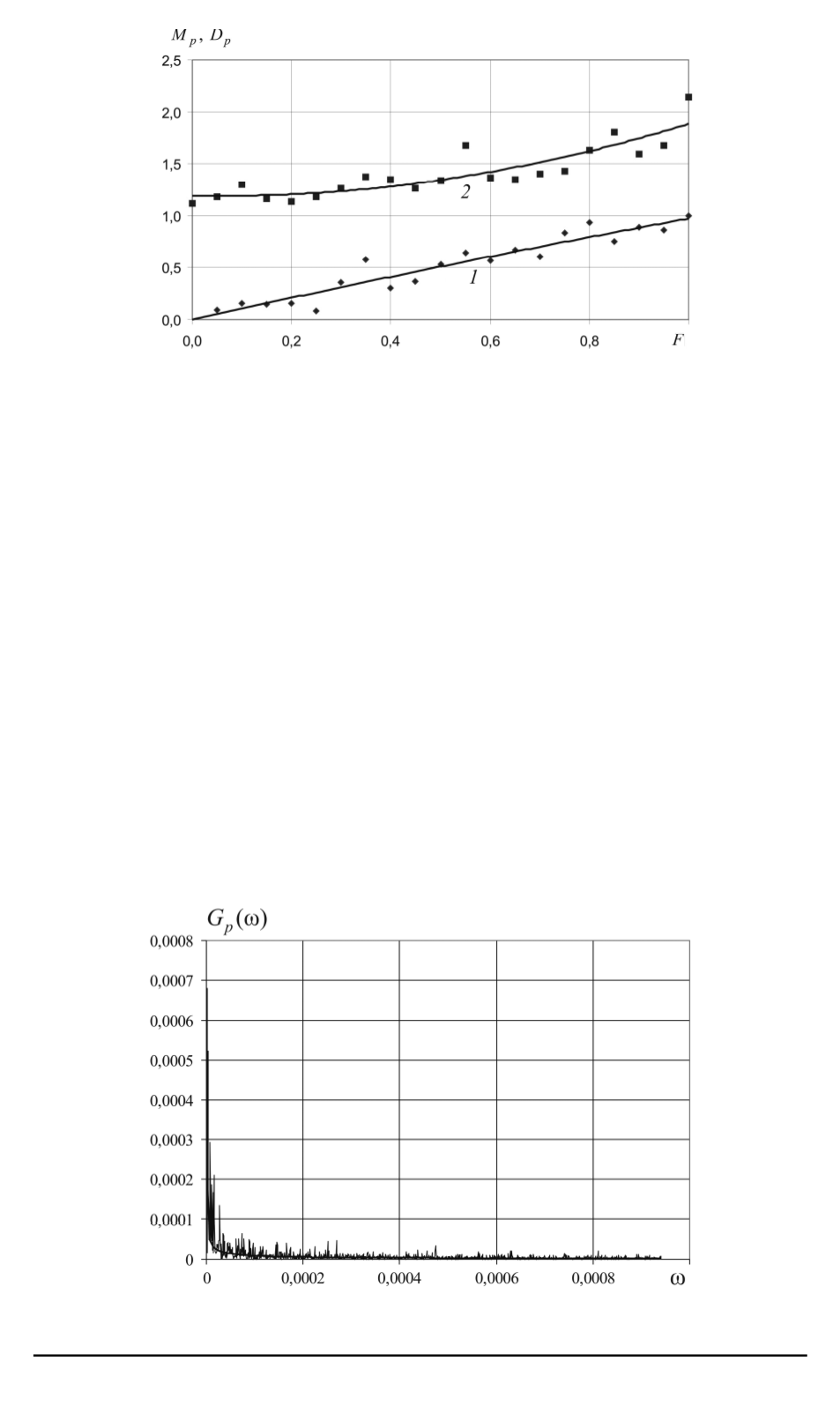
Рис. 1. Зависимость математического ожидания
M
p
(
1
) и дисперсии
D
p
(
2
) от
внешней силы
F
чений импульса
P
(
t
)
, по которым определялись математическое ожи-
дание
M
p
, дисперсия
D
p
и спектральная плотность
G
p
(
ω
)
процесса
P
(
t
)
.
На рис. 1 приведены зависимости математического ожидания
M
p
и дисперсии
D
p
флуктуаций импульса броуновской частицы
P
(
t
)
от
внешней приложенной силы
F
. Видно, что зависимость
M
p
(
F
)
имеет
линейный характер с коэффициентом пропорциональности, близким к
единице, что совпадает с традиционным описанием при
η
= 1
. Зависи-
мость дисперсии флуктуаций импульса
D
p
(
F
)
близка к квадратичной,
что связано с приближением средней скорости движения броуновской
частицы к средней квадратичной скорости ее хаотического движения.
На рис. 2 приведена спектральная плотность
G
p
(
ω
)
флуктуаций
импульса
P
(
t
)
для единичной внешней силы (
F
= 1
). Спектр рассчи-
тан по
2
∙
10
6
точкам. Из полученной зависимости
G
p
(
ω
)
следует, что
Рис. 2. Спектральная плотность флуктуаций импульса
P
(
t
)
при внешней силе
F
= 1
8
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2


