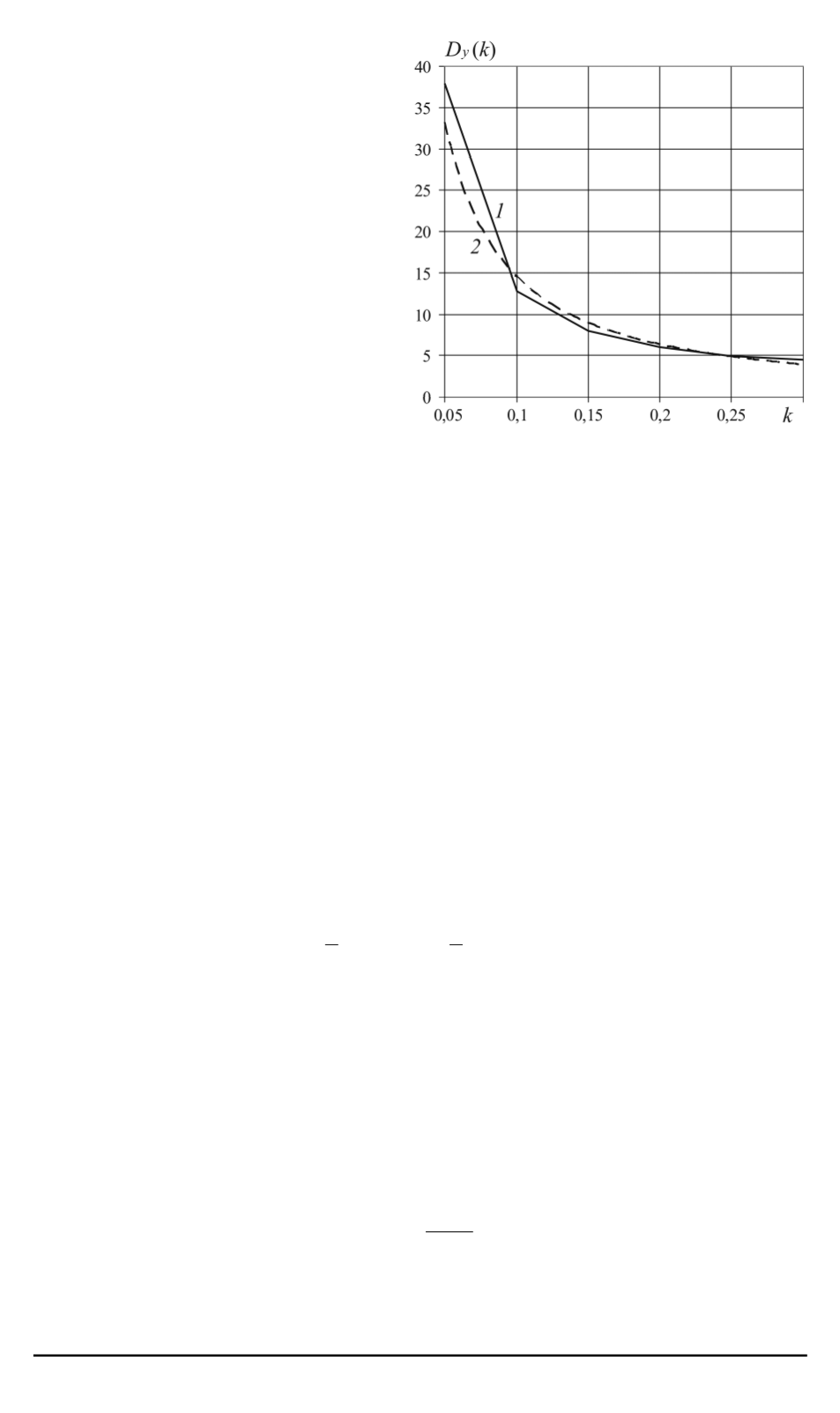
Рис. 4. Зависимость дисперсии флукту-
аций координаты
D
y
от коэффициента
упругости
k
при
F
= 0
(
1
) и степенная
функция аппроксимации (
2
)
При увеличении силы на
Δ
F
= 0
,
1
среднее значение ко-
ординаты частицы с большой
степенью точности увеличива-
ется на
Δ
Y
= 1
. Такое от-
клонение связано с выбором
k
,
так как из классического опи-
сания осциллятора следует, что
Δ
Y
= Δ
F/k
. Полученное со-
впадение с результатом клас-
сической теории служит одним
из подтверждений адекватности
используемой модели реально-
му процессу.
На рис. 4 изображена зави-
симость дисперсии флуктуаций
координаты
D
y
от коэффициен-
та упругости
k
при
F
= 0
. Вид-
но, что дисперсия уменьшается нелинейно с ростом
k
. Здесь же приве-
дена аппроксимирующая функция, соответствующая степенному зако-
ну (штриховая линия). Видно, что дисперсия флуктуаций координаты
уменьшается обратно пропорционально коэффициенту
k
. Полученное
с помощью метода наименьших квадратов уравнение аппроксимиру-
ющей кривой имеет вид
D
y
= 0
,
934
k
−
1
,
192
.
(30)
Согласно классической статистической теории на каждую из по-
ступательных и колебательных степеней свободы осциллятора прихо-
дится энергия
0
,
5
k
B
T
, т.е.
1
2
k Y
2
=
1
2
k
B
T.
(31)
Кроме того, в случае большого интервала реализации движения ос-
циллятора величина
h
Y
2
i
представляет собой дисперсию координаты:
D
y
=
Y
2
.
(32)
Выражение (32) следует из определения дисперсии
D
y
=
h
Y
2
i−h
Y
i
2
с
учетом того, что для осциллятора в отсутствие внешней силы
h
Y
i
= 0
.
Из соотношений (31) и (32) следует
D
y
=
k
B
T
k
.
(33)
Таким образом, зависимость дисперсии координаты классического ос-
циллятора
D
y
от коэффициента упругости
k
соответствует обратно
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2
11


