Новые переменные обращаются одновременно в нуль тогда и толь-
ко тогда, когда обращаются одновременно в нуль старые перемен-
ные, поэтому задача устойчивости по отношению к одним перемен-
ным эквивалентна задаче устойчивости по отношению к другим пере-
менным.
Система (18) удовлетворяет условиям теоремы, поэтому надо
найти младший член разложения функции
a
3
X
3
x
1
, C
(1)
2
x
1
,
0
,
0 +
+
a
4
X
4
x
1
, C
(1)
2
x
1
,
0
,
0
. После вычислений получаем:
a
3
X
3
x
1
, C
(1)
2
x
1
,
0
,
0 +
a
4
X
4
x
1
, C
(1)
2
x
1
,
0
,
0 =
−
1
6(
a
3
−
a
4
)
2
b
3
x
3
1
.
Коэффициент при
x
3
1
отрицательный, следовательно, нулевое по-
ложение равновесия системы (12) при условии
p <
1
2
b
2
+
29
12
асимпто-
тически устойчивое.
Численное моделирование.
Проверим полученные результаты
с помощью численного моделирования. Зададим следующие число-
вые значения параметров системы: коэффициент жесткости пружины
A
= 5
,
12
Н
м
, коэффициент демпфирования
B
= 0
,
4
Н
∙
с
м
, длина
каждого стержня
l
= 0
,
25
м; сосредоточенные массы
m
= 1
кг.
При таком выборе параметров коэффициент
b
= 0
,
5
, между реаль-
ным и безразмерным временем имеет место соотношение
t
≈
0
,
11
τ
.
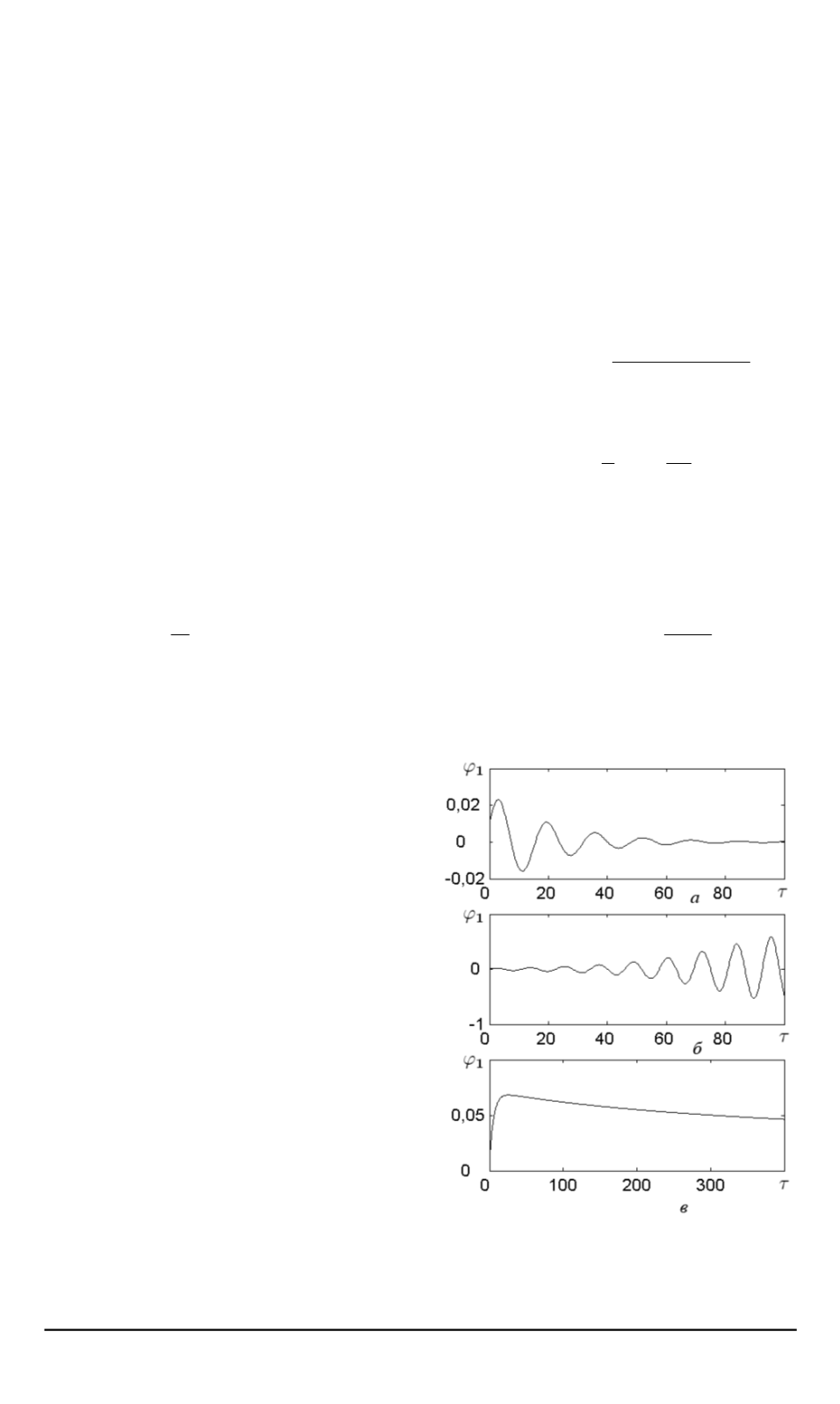
Рис. 6. Графики зависимости
ϕ
1
от
τ
:
a
—
f
= 0
,
5
,
p
= 1
;
б
—
p
= 2
;
в
—
f
= 1
,
p
= 1
Реальные и безразмерные силы
соотносятся следующим образом:
P
= 20
,
48
p
,
F
= 20
,
48
f
.
После приведения к безразмер-
ному виду решим систему диф-
ференциальных уравнений (6). На-
чальные условия примем следую-
щие:
ϕ
1
(0) = 0
,
01
,
ϕ
2
(0) = 0
,
01
,
ϕ
0
1
(0) = 0
,
01
,
ϕ
0
2
(0) = 0
,
01
.
Пусть безразмерная сила
f
= 0
,
5
. В этом случае значение
критической силы
˜
p
= 1
,
75
. Рас-
смотрим значение следящей силы
p
= 1
<
˜
p
. Оно меньше крити-
ческого значения, поэтому долж-
на иметь место асимптотическая
устойчивость, что и наблюдается
на рис. 6
а
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1
97


