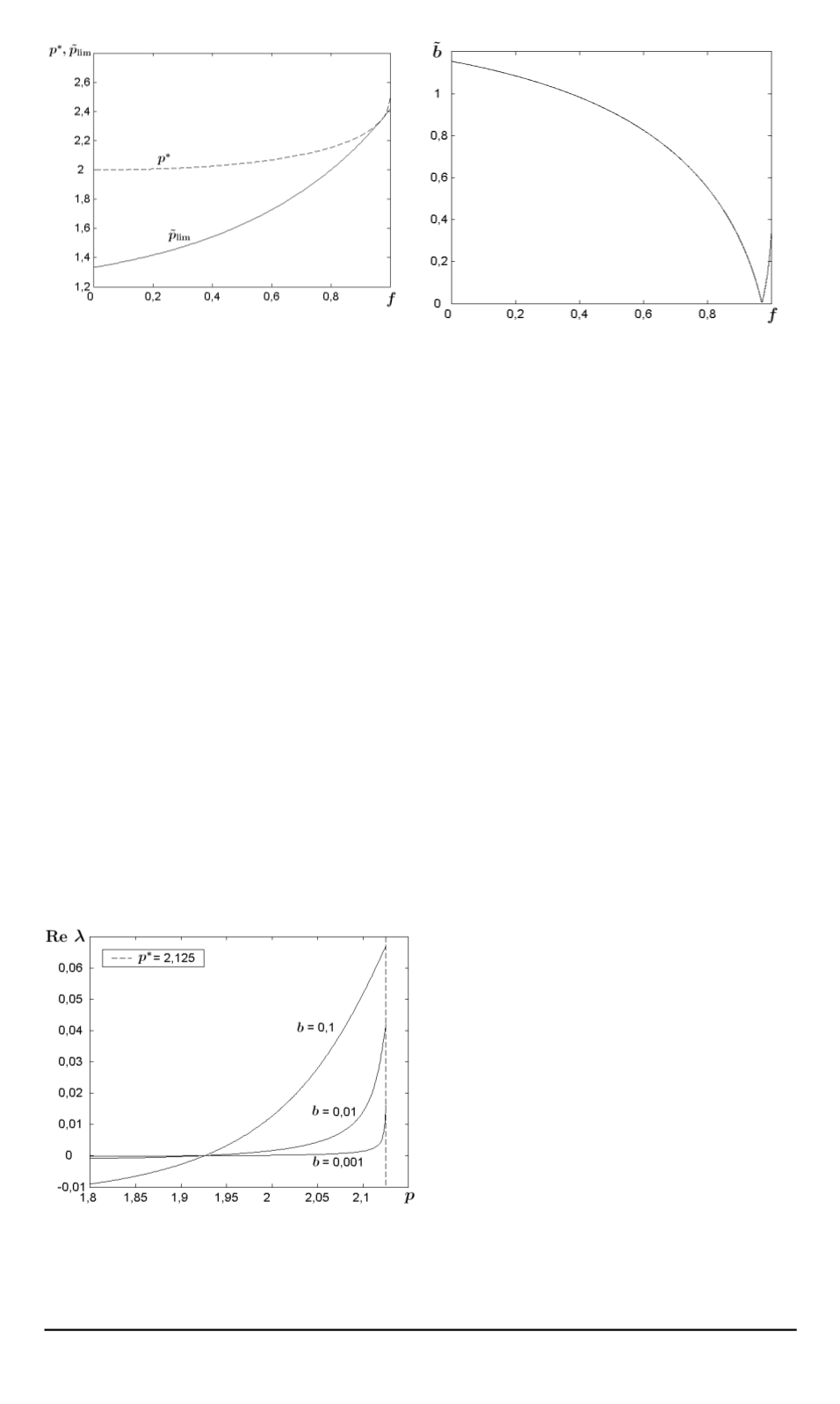
Рис. 3. Сравнение значения критиче-
ской силы в отсутствие вязкости с
предельным значением критической
силы при наличии демпфирования в
зависимости от консервативной си-
лы
f
Рис. 4. Зависимость коэффициента
˜
bb
˜
,
при котором совпадают величины
˜
p
и
p
, от силы
f
Заметим, что из устойчивости системы (9) не следует устойчивость
системы (6) при коэффициенте
B
= 0
. Отметим также, что доказать
устойчивость по Ляпунову системы (6) в нелинейной постановке при
отсутствии вязкости нельзя [5].
Анализ собственных значений.
Исследуем поведение собствен-
ных значений
λ
в зависимости от силы
p
при малом значении коэффи-
циента
b
, а также предельный переход критической силы
˜
p
. Поскольку
собственные значения
λ
непрерывны как функции
b
, то при стремле-
нии коэффициента
b
к нулю, они стремятся к собственным значениям
системы при
b
= 0
.
Значение потенциальной силы примем равным
f
= 0
,
75
, в этом
случае
p
= 2
,
125
.
На рис. 5 показана зависимость действительных частей корней ха-
рактеристического уравнения (8) от величины силы
p
Рис. 5. Зависимость собственных значе-
ний корней характеристического урав-
нения от силы
p
при некоторых малых значени-
ях
b
. При сравнительно больших
b
небольшое возрастание нагруз-
ки выше значения
˜
p
приводит к
заметному возрастанию действи-
тельных частей. Однако при ма-
лых
b
роль
˜
p
как критической
нагрузки уменьшается, посколь-
ку небольшое увеличение
p
вы-
ше значения
˜
p
уже не приводит к
большому увеличению Re
λ
. Су-
щественное возрастание Re
λ
те-
перь связано с малым увеличени-
92
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1


