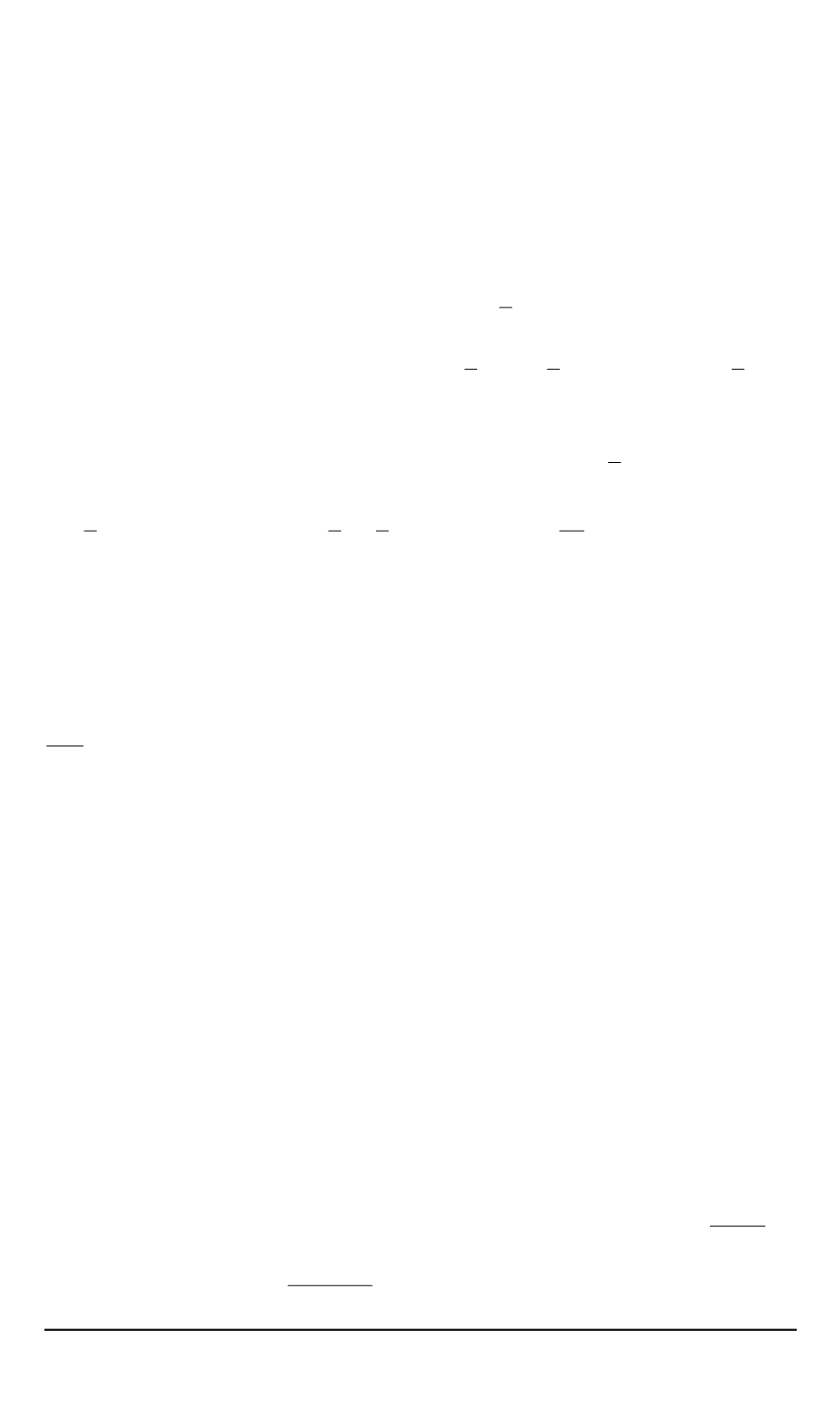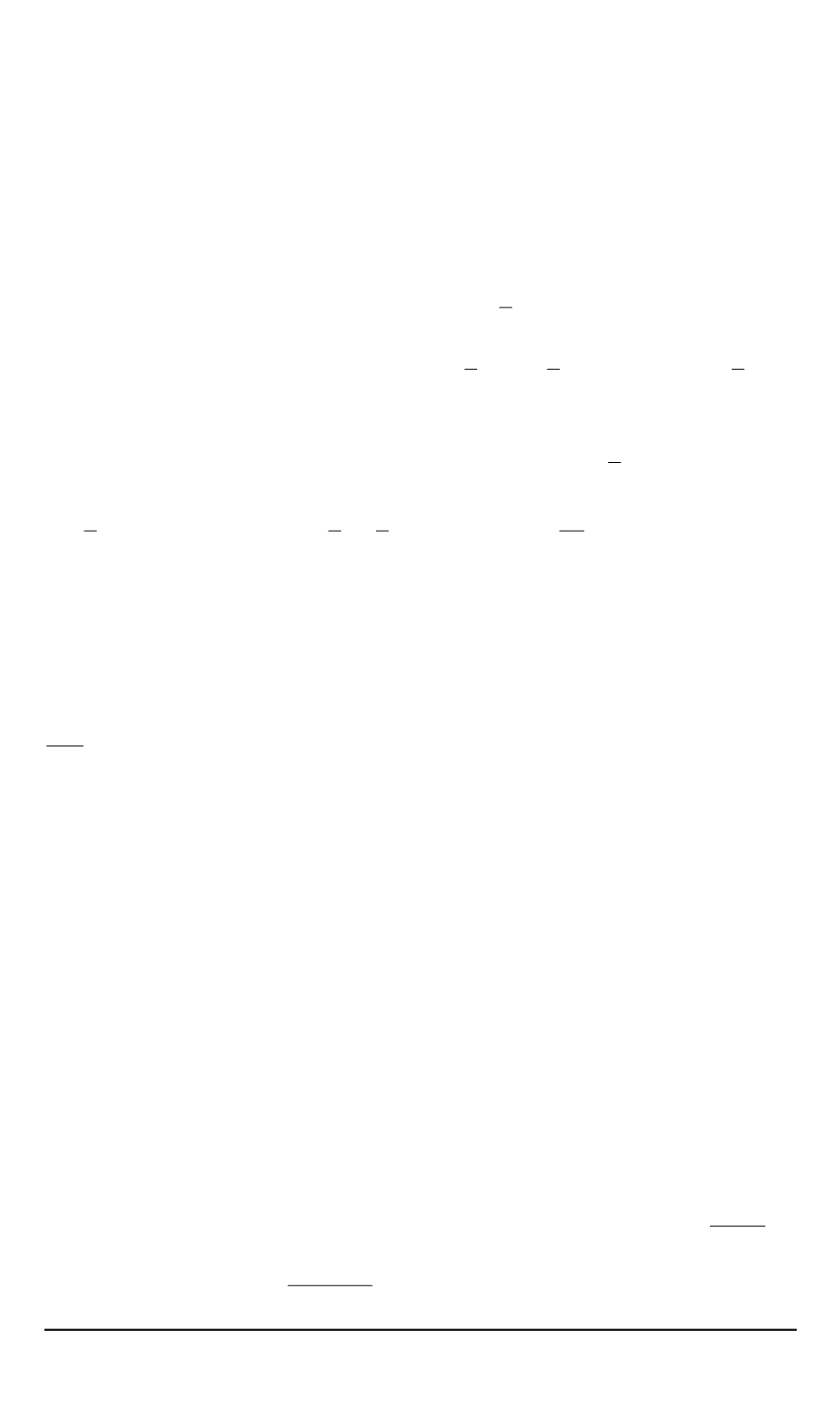
Получаем следующую систему:
z
0
1
=
z
3
,
z
0
2
=
z
4
,
z
0
3
= (
p
−
2)
z
1
+ (2
−
p
)
z
2
−
3
bz
3
+ 2
bz
4
+
Z
3
(
z
1
, z
2
, z
3
, z
4
)
,
z
0
4
= (3
−
p
)
z
1
+ (
p
−
3)
z
2
+ 4
bz
3
−
3
bz
4
+
Z
4
(
z
1
, z
2
, z
3
, z
4
)
,
(12)
где
Z
3
(
z
1
, z
2
, z
3
, z
4
) =
−
(
z
2
3
+
z
2
4
)(
z
1
−
z
2
) +
b
2
(7
z
3
−
5
z
4
)(
z
1
−
z
2
)
2
+
+
1
2
5
−
7
3
p
(
z
1
−
z
2
)
3
−
1
6
z
3
1
,
Z
4
(
z
1
, z
2
, z
3
, z
4
) = (2
z
2
3
+
z
2
4
)(
z
1
−
z
2
) +
b
−
5
z
3
+
7
2
z
4
(
z
1
−
z
2
)
2
+
+
5
3
p
−
4
z
1
(
z
1
−
z
2
)
2
+
7
2
−
5
3
p z
2
(
z
1
−
z
2
)
2
+
1
12
z
3
2
+ (2
z
1
−
z
2
)
3
.
Отметим, что если задачу не удастся решить, ограничиваясь слага-
емыми третьего порядка, то будет необходимо рассмотреть слагаемые
более высокого порядка.
Введем новую переменную
x
1
=
a
1
z
1
+
a
2
z
2
+
a
3
z
3
+
a
4
z
4
. Выби-
раем
a
i
так, чтобы для линейных слагаемых выполнялось равенство
dx
1
dτ
= 0
, т.е.
x
0
1
=
a
1
z
0
1
+
a
2
z
0
2
+
a
3
z
0
3
+
a
4
z
0
4
= 0
. Подставляя линей-
ные слагаемые из
z
0
1
,
z
0
2
,
z
0
3
,
z
0
4
и приравнивая нулю выражения при
z
k
,
получаем систему линейных однородных алгебраических уравнений:
(
p
−
2)
a
3
+ (3
−
p
)
a
4
= 0
,
(2
−
p
)
a
3
+ (
p
−
3)
a
4
= 0
,
a
1
−
3
ba
3
+ 4
ba
4
= 0
,
a
2
+ 2
ba
3
−
3
ba
4
= 0
.
(13)
Поскольку мы рассматриваем случай, когда характеристическое
уравнение имеет один нулевой корень, то определитель системы (13)
равен нулю, и, следовательно, система всегда имеет ненулевое ре-
шение. Покажем, что всегда существует решение системы (13), при
котором
a
1
6
= 0
.
1. Если
p
= 2
, то полагаем
a
3
6
= 0
,
a
4
= 0
, следовательно,
a
1
= 3
ba
3
6
= 0
.
2. Если
p
6
= 2
, то полагаем
a
4
6
= 0
, следовательно,
a
3
=
3
−
p
2
−
p
a
4
,
откуда получаем
a
1
=
b
(
p
+ 1)
2
−
p
a
4
6
= 0
, так как
b >
0
, p
≥
0
.
94
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1