Отметим также статью [5], где в нелинейной постановке решена
задача устойчивости положения равновесия маятника Циглера в кри-
тическом случае устойчивости пары чисто мнимых корней, т.е. когда
следящая сила имеет критическое значение.
Следует заметить, что парадокс дестабилизации возникает и в кон-
тинуальных моделях. Обзор результатов, посвященных этому вопросу,
а также других результатов, связанных с парадоксом дестабилизации,
приведен в работе [6].
Статья [7] посвящена качественному и численному описанию па-
радоксального поведения неконсервативных систем под действием ма-
лых диссипативных и гироскопических сил. Для объяснения парадок-
са дестабилизации исследуется движение корней характеристического
уравнения на комплексной плоскости. Получена функциональная за-
висимость критической нагрузки от параметров диссипативных и ги-
роскопических сил, позволяющая определять скачок для критической
нагрузки.
В настоящей работе, состоящей из двух частей, рассмотрен ма-
ятник Циглера, дополнительно нагруженный консервативной силой.
В первой части показано, какое влияние на парадокс дестабилизации
оказывает добавление консервативной силы. Во второй части исследо-
вана устойчивость нулевого положения равновесия в критическом слу-
чае одного нулевого корня, который возникает вследствие добавления
консервативной силы. Отметим, что в данной работе рассматривается
устойчивость по Ляпунову.
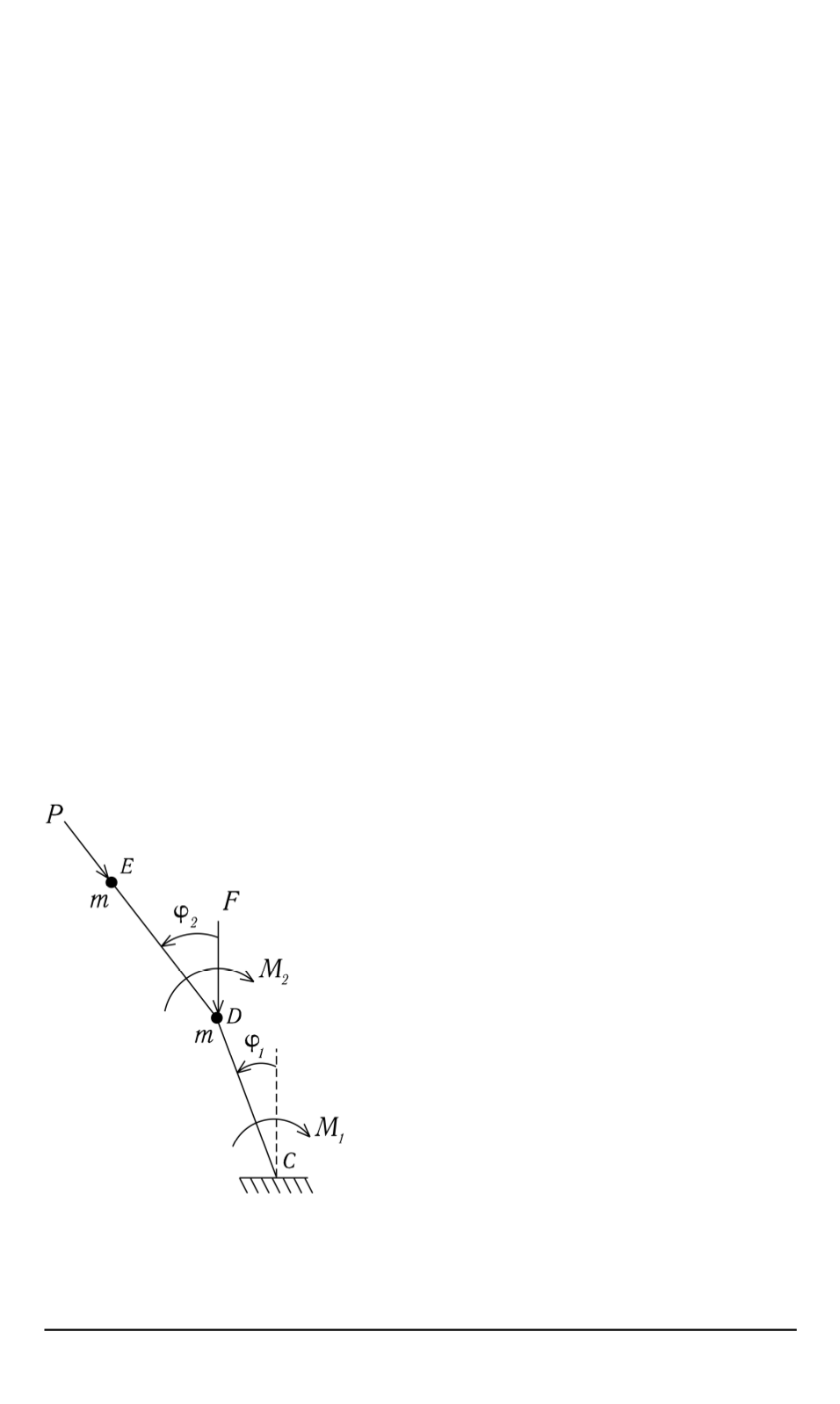
Рис. 1. Двойной маятник под
действием консервативной (
F
)
и следящей (
P
) сил
Уравнения движения маятника.
Двойной маятник представляет собой
систему двух невесомых стержней
CD
и
DE
длиной
l
(рис. 1). Шарни-
ры обладают вязкоупругими свойства-
ми, так что восстанавливающие момен-
ты в них равны
M
1
=
−
Aϕ
1
−
B
˙
ϕ
1
,
M
2
=
−
A
(
ϕ
2
−
ϕ
1
)
−
B
( ˙
ϕ
2
−
˙
ϕ
1
)
. В
шарнире
D
и на свободном конце
E
расположены две одинаковые массы
m
.
Гравитационные силы отсутствуют. На
свободный конец маятника
E
действует
следящая сила
P
, направление которой
во всe время движения совпадает с на-
правлением стержня
DE
. На шарнир
D
действует консервативная сила
F
, все-
гда направленная вертикально вниз.
88
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1


