уравнение, определяющее модулятор,
ε 1
−
c
1
σ (
x
−
y
)
c
2
(
−
y
+
r x
−
x z
)
c
3
(
−
bz
+
x y
)
=
f
(
X
, η) .
Из условия простоты модулятора и минимальности числа связей
определяем элементы матрицы
C
:
c
1
=
1
,
c
2
=
0
,
c
3
=
0
. В результате
получаем вектор
f
(
X
, μ
t
)
=
(
−
ε1 (μ
t
) σ (
x
−
y
) ,
0
,
0
)
т
. Осциллятор
Лоренца с фазовой модуляцией хаотической несущей имеет вид
˙
x
= −
(
1 +
με 1 (μ
t
)) σ (
x
−
y
)
;
˙
y
= −
y
+
r x
−
x z
;
˙
z
= −
bz
+
x y
.
(25)
Информационный сигнал
1 (μ
t
)
может быть любой ограниченной
гладкой функцией. Возможно, что данный сигнал сам может быть
реализацией случайного процесса.
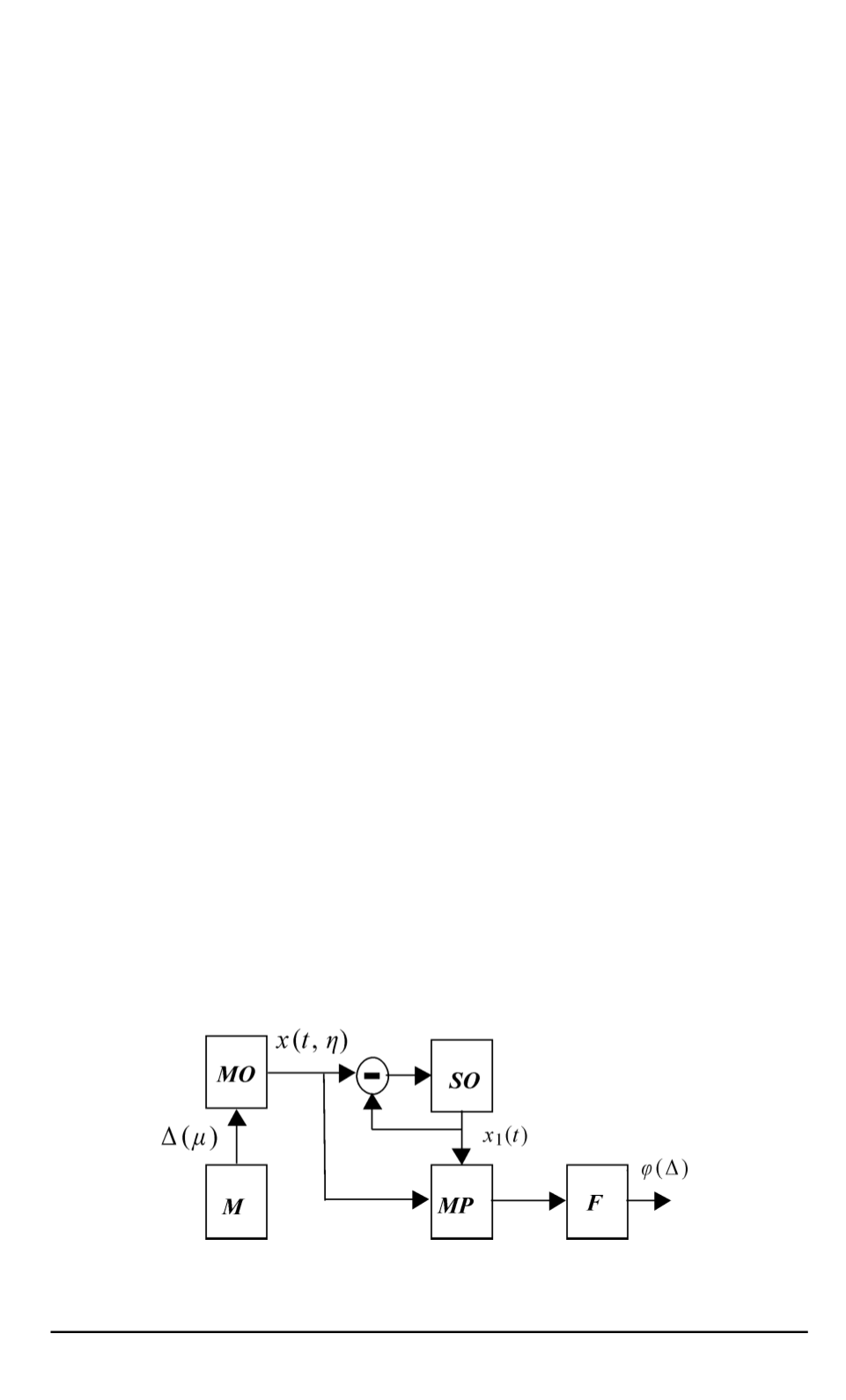
На рис. 2 приведена элементарная блок-схема передачи информа-
ции при непосредственной синхронизации автогенераторов с фазовым
детектированием полезного сигнала. На рис. 3 приведены результа-
ты численного эксперимента, проведенного по схеме рис. 2. Ведущим
автогенератором является осциллятор Лоренца (25), модулированный
периодическим сигналом
1 (μ
t
)
=
A
sin
μω
t
. Параметры системы Ло-
ренца:
σ
=
10
,
r
=
27
,
b
=
8
/
3
. Подстраиваемым автогенератором
является невозмущенный осциллятор Лоренца с теми же параметра-
ми. Связь осцилляторов осуществляется согласно уравнениям (23) с
матрицей
C
=
diag
(
1
,
0
,
0
)
. Фильтр является резонансным. На рис. 3,
а
проиллюстрирован режим биений автогенераторов, параметр связи
ε
=
0
,
5
мал и, тем самым, подстраиваемый автогенератор находит-
ся вне полосы удержания синхронизации. На плоскости
(1, ϕ (1))
Рис. 2. Блок-схема передачи информации:
MO
— ведущий автогенератор;
SO
— подстраиваемый автогенератор;
M
— модулятор;
MP
— умножающее устройство;
F
— фильтр
94
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4


