задано осевое смещение
u
2
e
=
ε
max
z
max
, где
ε
max
— средняя дефор-
мация сжатия амортизатора, на поверхности
z
= 0
задано свободное
скольжение, поверхность
r
=
f
(
z
)
свободна от нагрузок, а на оси
симметрии заданы условия симметрии
z
= 0 :
T
rz
= 0
, u
z
= 0;
z
max
= 0 :
T
rz
= 0
, u
z
=
u
2
e
;
r
= 0 :
T
rz
= 0
, u
r
= 0;
r
=
f
(
z
) :
T
rz
=
T
rr
= 0
.
(39)
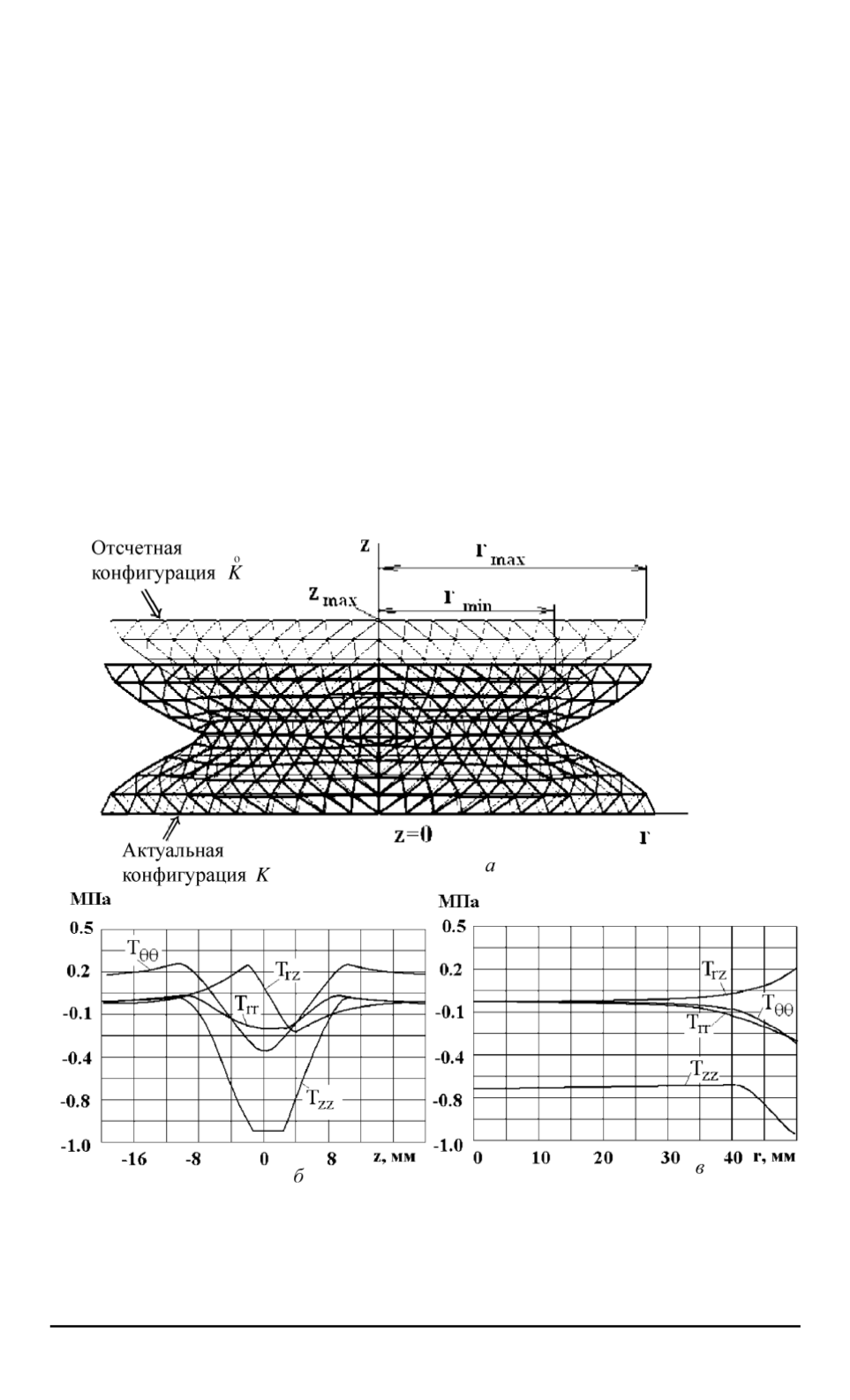
На рис. 4,
а
показана конечно-элементная сетка для амортизато-
ра в отсчетной и актуальной (деформированной) конфигурациях.
На рис. 4,
б, в
и 5–7 приведены результаты расчетов напряжений в
амортизаторе при следующих значениях параметров:
l
1
= 1
МПа,
l
2
= 10
МПа, высота
z
max
= 20
мм, максимальный и минимальный
радиусы
r
max
= 40
мм,
r
min
= 10
мм. Расчет проведен для значений
ε
max
, равных
−
0
,
1
,
−
0
,
5
−
5
и
−
10
%.
Рис. 4. Конечно-элементная сетка для амортизатора в отсчетной и актуальной
конфигурациях при осевом сжатии (
a
), распределение напряжений по осевой
координате
z
на свободной поверхности амортизатора (
б
) и по радиальной ко-
ординате
r
в зоне утонения амортизатора (
в
) при деформации осевого сжатия
2,5%
78
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3


