Рис. 2. Конечно-элементная сетка для
цилиндра в отсчетной и актуальной кон-
фигурациях под действием внутреннего
давления (задача Ламе)
сравнительные расчеты, дает
лучшее качество решения с точ-
ки зрения сохранения симме-
трии относительно плоскости
z
=
1
2
z
max
и устойчивости ите-
рационного процесса по сравне-
нию с типовой нерегуляризиро-
ванной КЭ сеткой, характерной
для стандартных коммерческих
КЭ-пакетов.
Результаты расчетов.
Те-
стирование разработанного ме-
тода проводилось путем срав-
нения численных результатов с
аналитическим решением нели-
нейной задачи Ламе [1] о трубе,
нагруженной внутренним давлением, торцы которой свободно сколь-
зят по плоскостям
z
= 0
и
z
=
z
max
, внешняя поверхность цилиндра
свободная. На рис. 2 показана КЭ сетка для цилиндра в отсчетной и
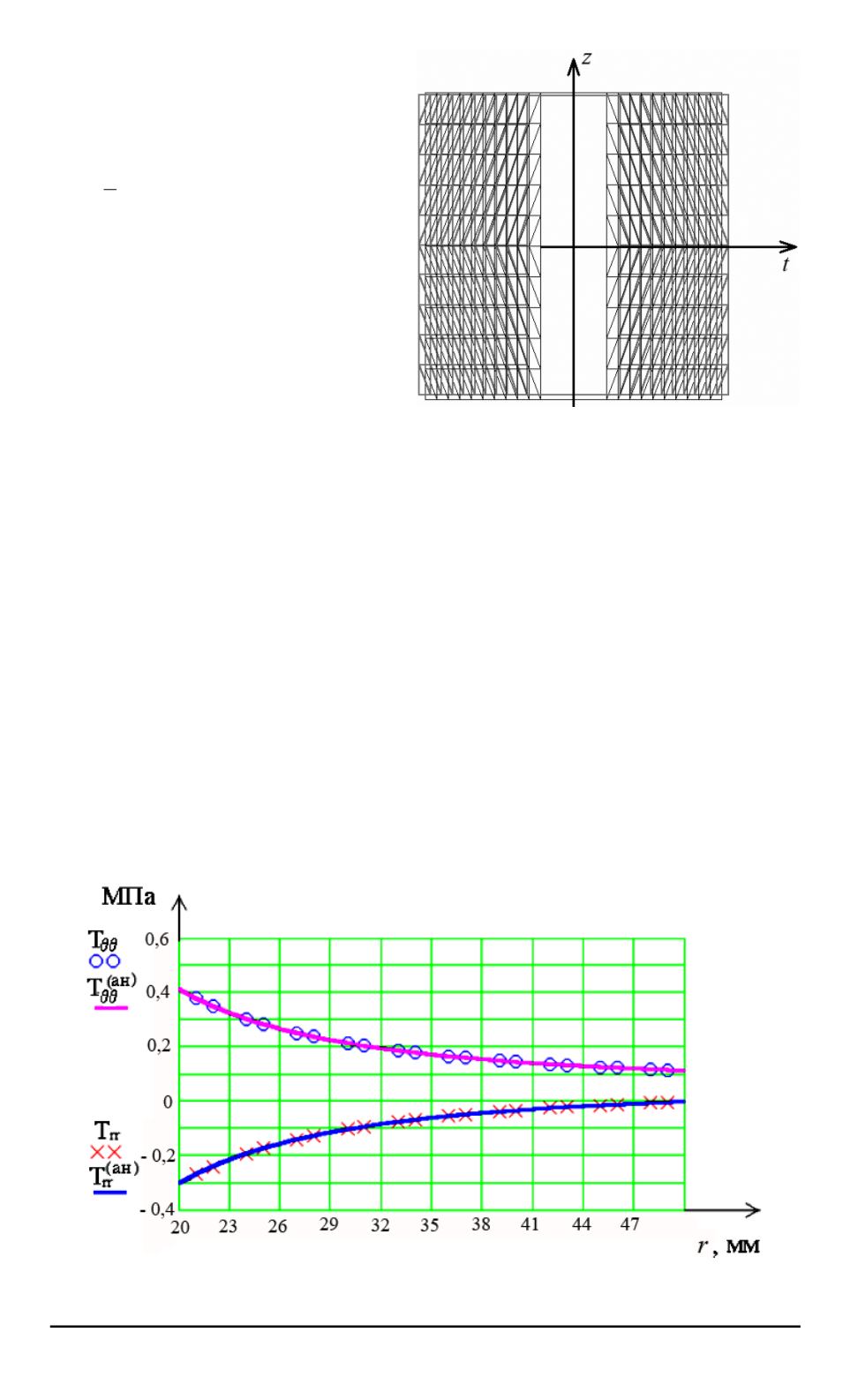
актуальной конфигурациях, а на рис. 3 — распределение радиальных
и окружных напряжений в зависимости от радиальной координаты
r
.
Получено хорошее совпадение аналитических и численных результа-
тов, относительная ошибка не превышает 0,1%.
Далее разработанный метод применен для расчета напряжений в
осесимметричном амортизаторе, работающем при осевом сжатии. Гра-
ничные условия заданы в следующем виде: на поверхности
z
=
z
max
Рис. 3. Распределение радиальных и окружных напряжений в задаче Ламе, по-
лученных конечно-элементным расчетом и по аналитическому решению
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3
77


