Математическое обоснование получения упорядоченных структур на основе частиц сферической формы - page 14

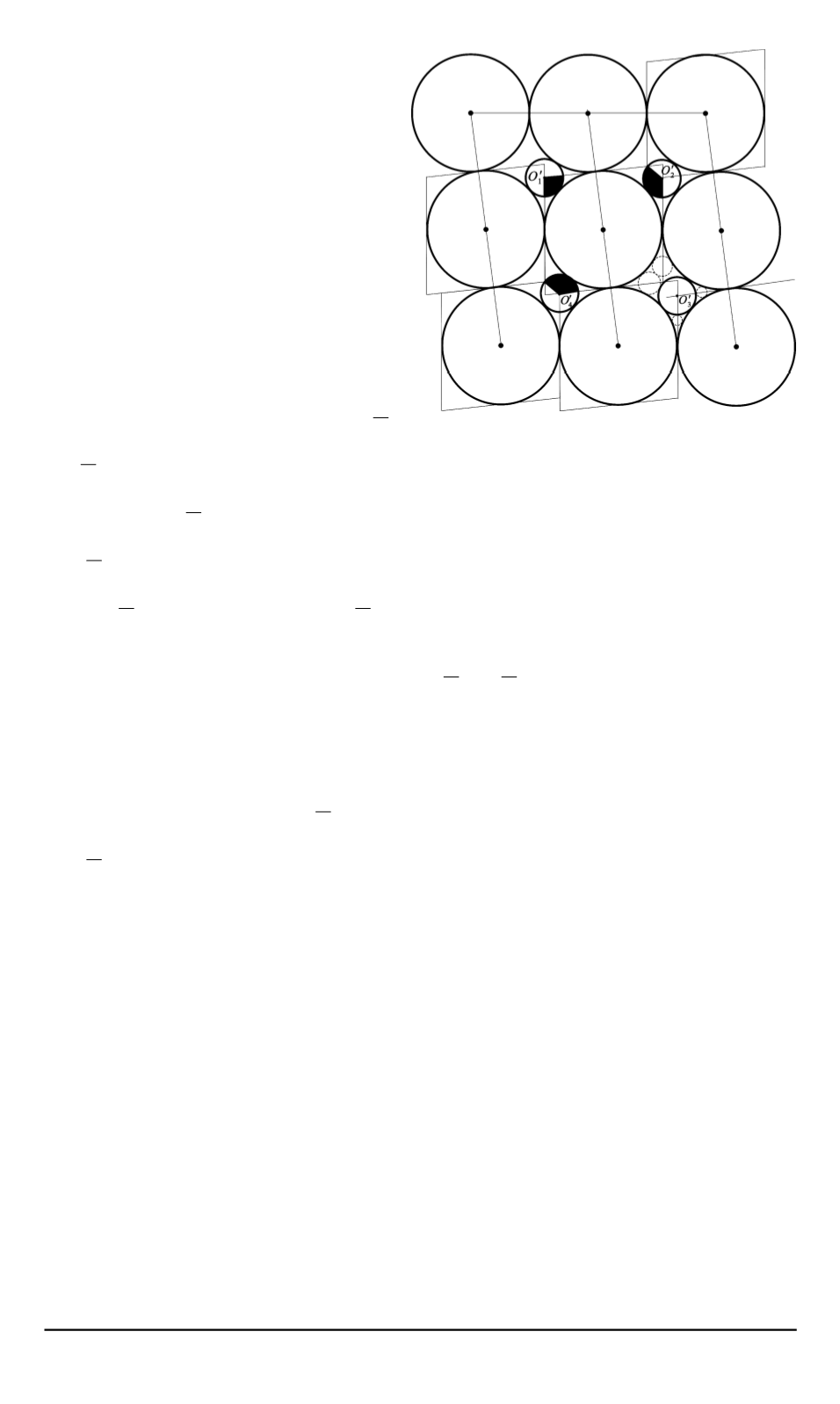
Рис. 14. Схема упаковки при
αкр < α < 90◦
Выводы. 1. Математически
обоснован выбор расчетной мо-
дели — фундаментальной ячей-
ки и проведен расчет плотности
ее упаковки при различных зна-
чениях определяющего параме-
тра (угла α взаимного располо-
жения фундаментальных ячеек).
2. На основе расчетов уста-
новлено, что плотность упаков-
ки фундаментальной ячейки δ0
при возрастании угла α с π
3
до π
2
монотонно убывает от ве-
личины δ0
π
3 ≈ 0,6046 до
δ0
π
2 ≈ 0, 5236 без цилиндрических наполнителей и увеличивается
от δ 1
π
3 ≈ 0,64801 до δ1
π
2 ≈ 0, 65835 с цилиндрическим напол-
нителем.
3. В области изменения угла α от π
3
до π
2
найден критический угол
αкр ≈ 77,337◦, при котором не нарушаются условия существования
фундаментальной ячейки и одновременного размещения в области
между шарами двух цилиндрических наполнителей. Для этого слу-
чая функция δ1 ( α) при π
3
< α < α строго монотонно убывает от
δ1
π
3 ≈ 0, 648 до δ1 ( α ) ≈ 0,637, а в области α < α < αкр возраста-
ет от δ1 (α ) ≈ 0,637 до δ1 (α кр) ≈ 0, 665.
СПИСОК ЛИТЕРАТУРЫ
1. С т о я н Ю. Г., Я к о в л е в С. В. Математические модели и оптимизаци-
онные методы геометрического проектирования. – Киев: Наук. думка, 1986. –
268 с.
2. С т о я н Ю. Г., Г и л ь Н. И. Свойства и способы реализации функции
плотного размещения. – Киев: АН УССР, 1972. – 48 с.
3. К о н в е й Д ж., С л о э н Н. Упаковки шаров, решетки и группы. В 2-х
томах. Т. 1. – М.: Мир, 1990. – 415 с. Т. 2. – 376 с.
4. Т о т Л. Ф. Расположения на плоскости, на сфере и в пространстве. – М.:
ГИФМЛ, 1958. – 364 с.
Статья поступила в редакцию 13.06.2006
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 2 91