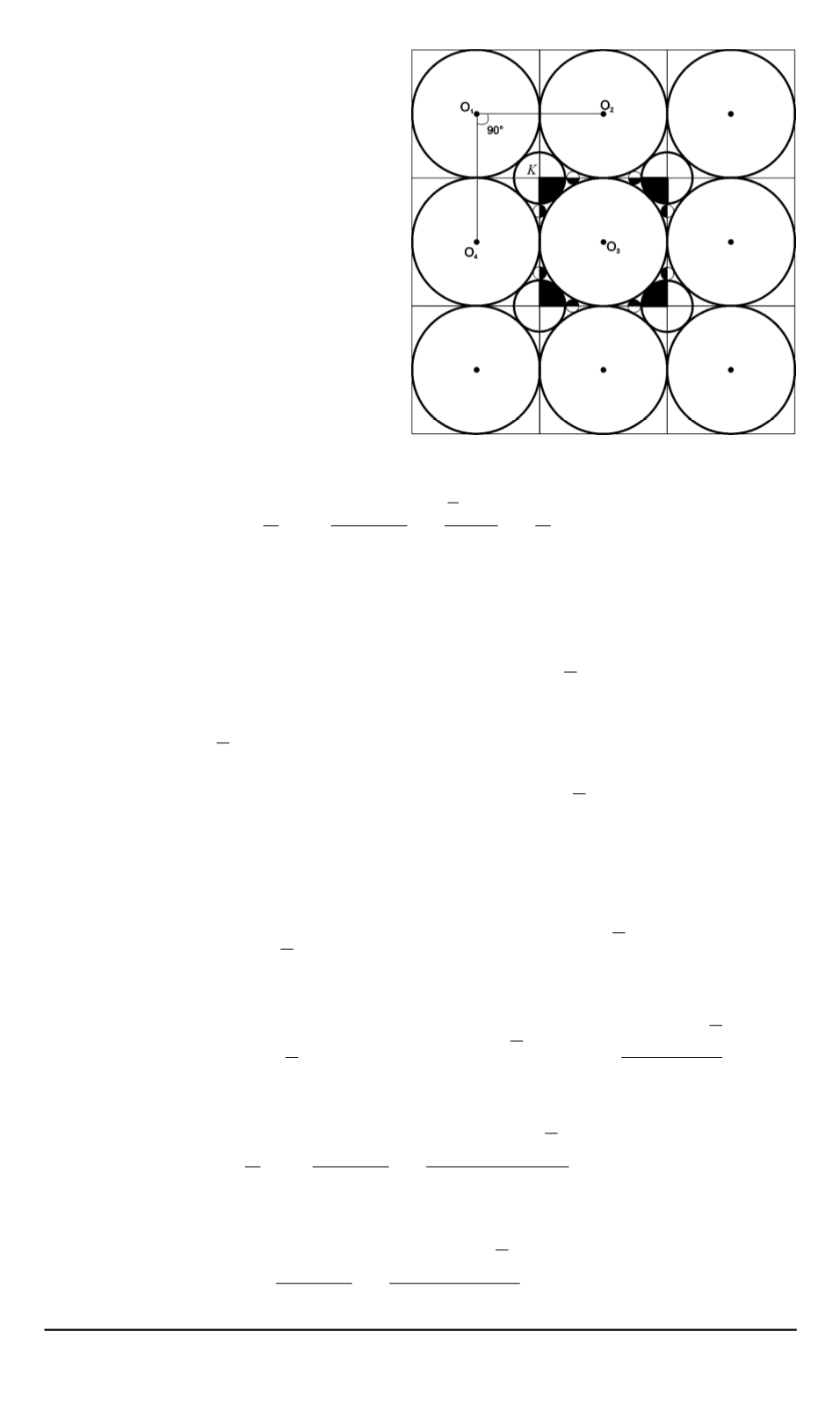
Рис. 4. Схема упаковки
α
= 90
◦
Вариант 1.
α
= 90
◦
(см.
рис. 2, рис. 4). Вначале вычи-
слим плотность этой упаковки.
При
α
= 90
◦
фундаменталь-
ной ячейкой является прямо-
угольный параллелепипед вы-
сотой
2
r
, основанием которого
служит квадрат со стороной
2
r
(описанный около окружности
радиуса
r
)
площадью
S
кв
= 4
r
2
,
т.е. куб объемом
(2
r
)
3
.
Тем самым плотность перво-
начальной упаковки
δ
0
=
δ
0
π
2
=
V
шара
V
фунд.яч.
=
4
3
πr
3
(2
r
)
3
=
π
6
≈
0
,
52360
.
Обозначим через
x
радиус прямого кругового цилиндра (цилин-
дрического наполнителя) с основаниями на нижней и верхней плоско-
стях, касающегося шаров с центрами в точках О
1
, О
2
, О
3
, О
4
внешним
образом (см. рис. 4). Вычисления дают
x
=
r
√
2
−
1
.
Следовательно, объем цилиндра высотой
2
r
, радиус основания ко-
торого
x
=
r
√
2
−
1
,
V
цил.х
=
πx
2
∙
2
r
=
πr
3
2 3
−
2
√
2
.
В каждую фундаментальную ячейку попадают четыре четвертинки
таких цилиндров суммарным объемом
V
x
= 4
∙
1
4
V
цил.x
=
V
цил.x
= 2
πr
3
3
−
2
√
2
.
Тем самым объем тел, попавших в фундаментальную ячейку,
V
1
=
V
ш
+
V
x
=
4
3
πr
3
+ 2
πr
3
3
−
2
√
2 = 2
πr
3
11
−
6
√
2
3
,
а плотность упаковки стала равной
δ
1
=
δ
1
π
2
=
V
1
V
фунд.яч.
=
π
11
−
6
√
2
12
≈
0
,
65835
.
Добавка к плотности составила
Δ
1
δ
=
V
x
V
фунд.яч.
=
π
3
−
2
√
2
4
≈
0
,
13475
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 2
81


