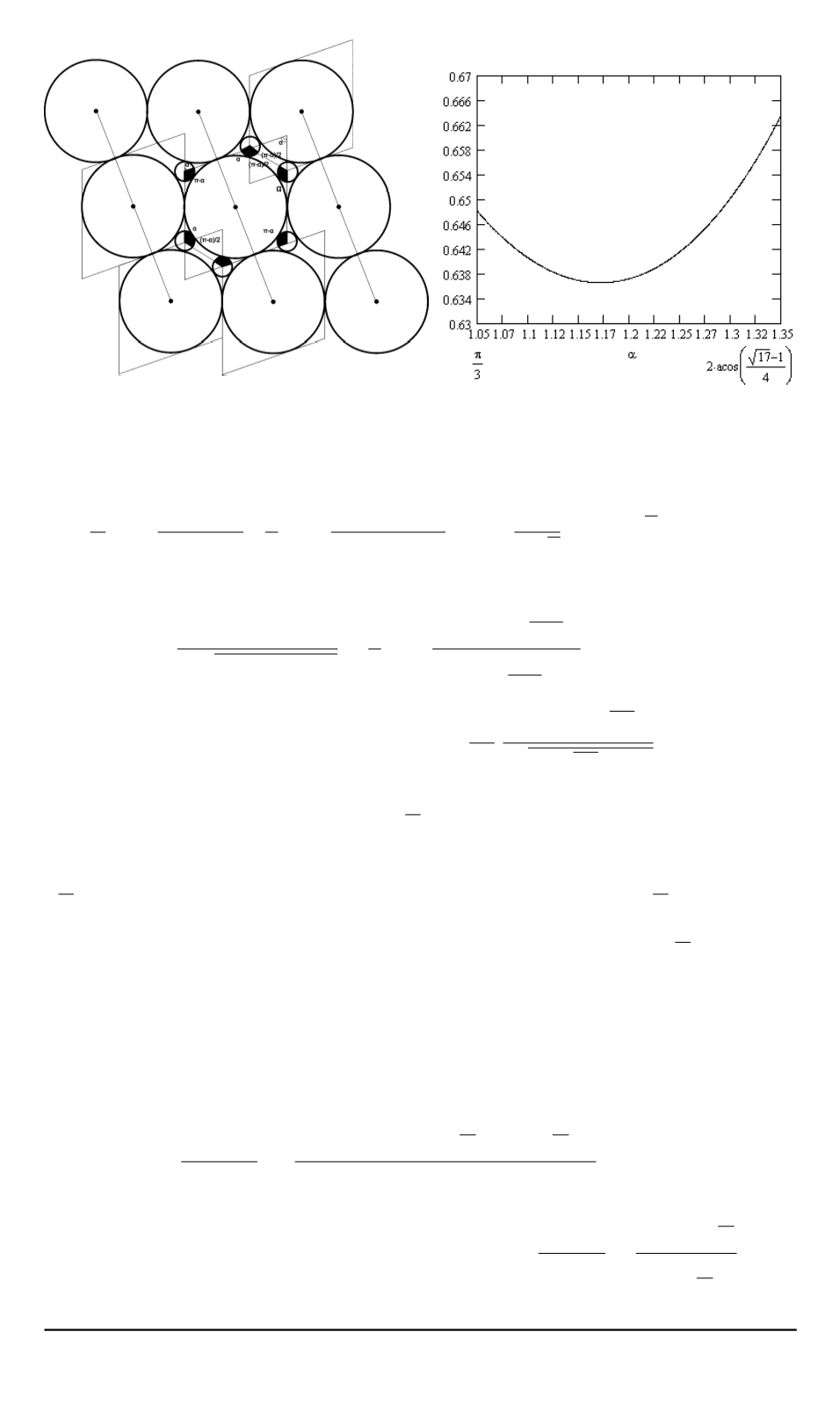
Рис. 9.
Схема упаковки при
60
◦
< α
≤
α
кр
Рис. 10. График функции
δ
1
(
α
)
В частности,
δ
1
π
3
=
π
2 sin 60
◦
1
3
+
1
−
cos 30
◦
cos 30
◦
=
4
π
3
√
3
2
− √
3
≈
0
,
64801;
δ
1
(
α
кр
) =
π
2
p
1
−
cos
2
α
кр
1
3
+
1
−
cos
α
кр
2
cos
α
кр
2
2
=
=
π
12
47
−
9
√
17
p
10
√
17
−
26
≈
0
,
66357
.
График функции
δ
1
(
α
)
при
α
2
h
π
3
;
α
кр
i
приведен на рис. 10.
Исследования показывают, что функция
δ
1
(
α
)
имеет на отрезке
h
π
3
;
α
кр
i
единственный минимум
α
≈
1
,
169
, т.е. при
π
3
< α < α
функция
δ
1
(
α
)
строго монотонно убывает от величины
δ
1
π
3
≈
0
,
648
до
δ
1
(
α
)
≈
0
,
637
, а при
α < α < α
кр
— возрастает от
δ
1
(
α
)
≈
0
,
637
до
δ
1
(
α
кр
)
≈
0
,
665
.
Вернемся к задаче о вычислении плотности упаковки. Добавка к
плотности составила
Δ
1
δ
(
α
) =
V
x
V
фунд.яч.
=
4
πr
3
1
−
cos
α
2
.
cos
α
2
2
8
r
3
sin
α
=
=
π
2 sin
α
1
−
cos
α
2
cos
α
2
2
.
88
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 2


