и это увеличение составило
Δ
2
δ
δ
1
∙
100% =
25
121
42
−
15
√
3 %
≈
3
,
31 %
.
По сравнению с первоначальной плотностью увеличение составило
Δ
2
δ
δ
0
∙
100% =
129
−
72
√
3
121
∙
100%
≈
3
,
547 %
,
что в 2 раза меньше, чем увеличение плотности упаковки на первом
этапе.
Вариант 3.
60
◦
< α <
90
◦
. Вначале вычислим плотность этой
упаковки. При
60
◦
< α <
90
◦
фундаментальной ячейкой является пря-
мая шестиугольная призма высотой
2
r
, основанием которой служит
шестиугольник
ABCDEF
(см. рис. 6), площадь которого
S
осн
=
S
BTEU
−
2
S
Δ
AFU
=
4
r
2
sin
α
−
4
r
2
cos
2
α
sin
α
=
4
r
2
sin
α
1
−
cos
2
α
= 4
r
2
sin
а объем фундаментальной ячейки
V
фунд.яч.
=
S
осн.
∙
2
r
= 4
r
2
sin
α
∙
2
r
= 8
r
3
sin
α.
Тем самым плотность первоначальной упаковки
δ
0
=
δ
0
(
α
) =
V
шара
V
фунд.яч.
=
4
3
πr
3
8
r
3
sin
α
=
π
6 sin
α
.
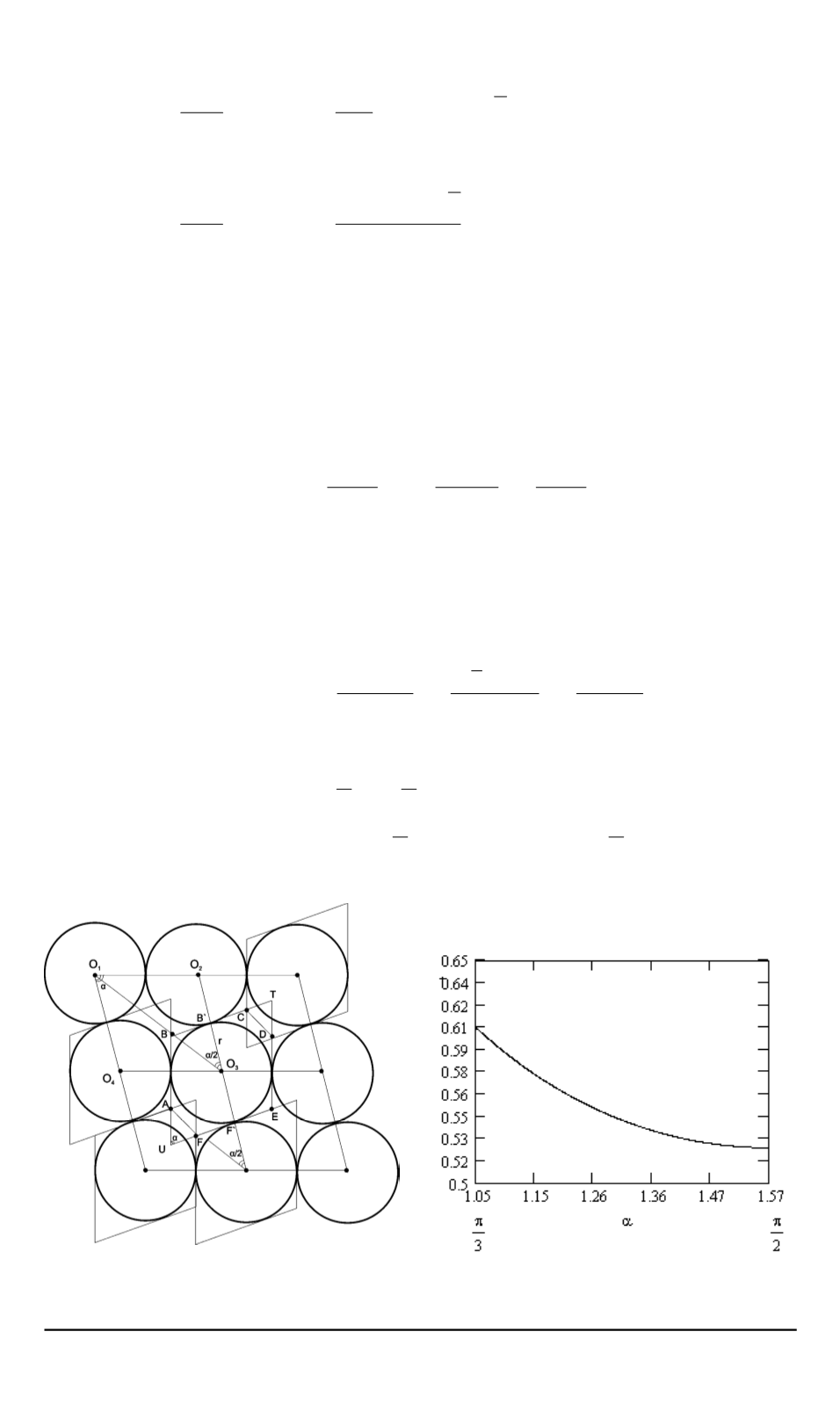
График функции
δ
0
(
α
)
изображен на рис. 7.
При возрастании
α
от
π
3
до
π
2
плотность упаковки строго моно-
тонно убывает от величины
δ
0
π
3
≈
0
,
6046
до
δ
0
π
2
≈
0
,
5236
.
Рис. 6.
Схема упаковки при
60
◦
< α <
90
◦
Рис. 7. График функции
δ
0
(
α
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 2
85


