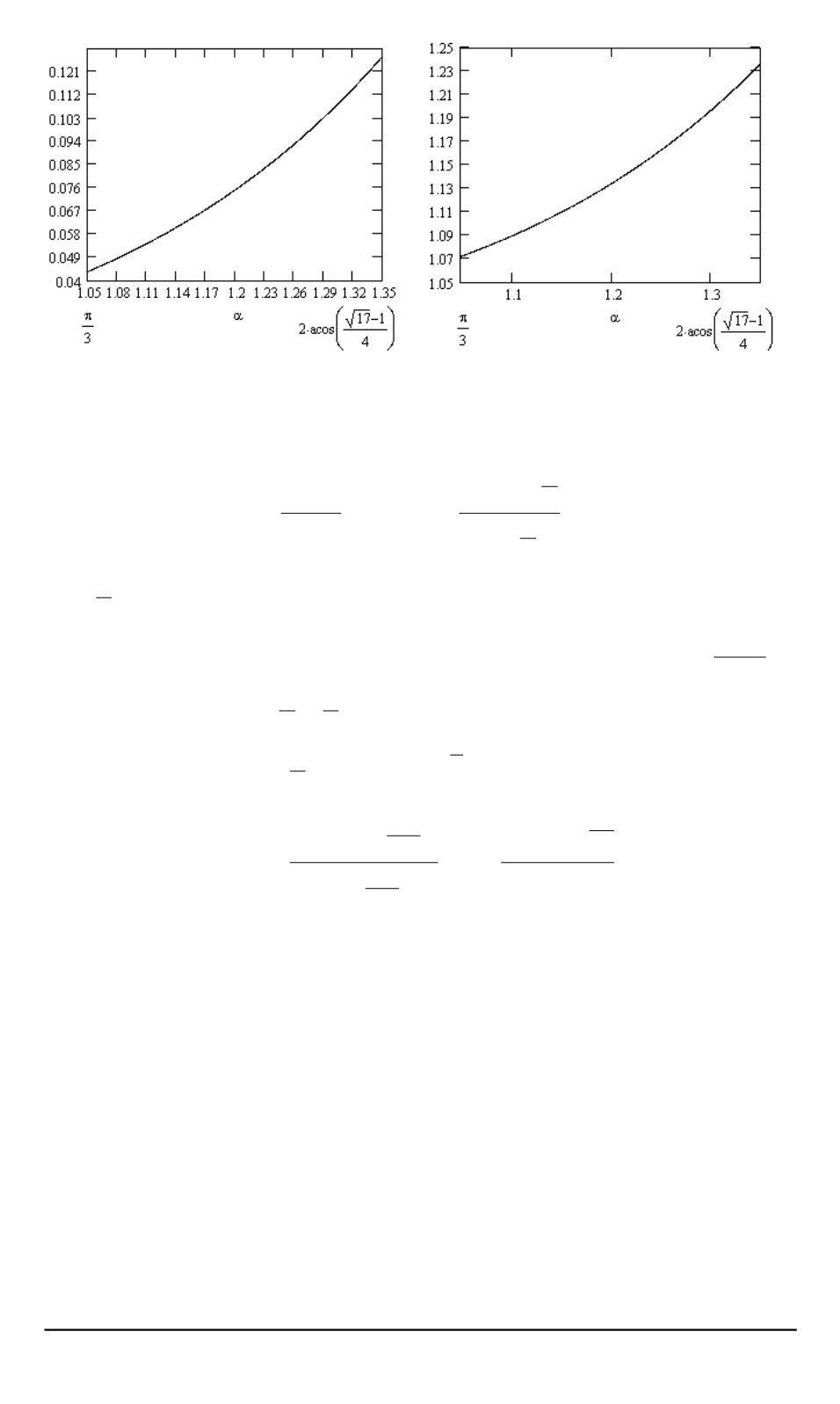
Рис. 12. График функции
Δ
1
δ
(
α
)
Рис. 13. График функции
k
(
α
)
График функции
Δ
1
δ
(
α
)
изображен на рис. 12.
Плотность первоначальной упаковки возросла в
k
(
α
) =
δ
1
(
α
)
δ
0
(
α
)
= 1 + 3
1
−
cos
α
2
cos
α
2
2
раз
.
При
π
3
6
α
6
α
кр
эта функция строго монотонно возрастает как супер-
позиция строго монотонно убывающих функций
h
(
t
) = 1+3
1
−
t
t
2
(0
< t <
1)
и
t
= cos
α
2
(
π
3
6
α
6
α
кр
)
. При этом
k
π
3
= 4 2
− √
3
≈
1
,
0718
,
k
(
α
кр
) = 1 + 3
1
−
cos
α
кр
2
cos
α
кр
2
2
=
47
−
9
√
17
8
≈
1
,
23650
.
График функции
k
(
α
)
изображен на рис. 13
Случай
α
кр
< α <
90
◦
. При
α
≈
90
◦
в оставшуюся область входят
два одинаковых цилиндра радиусом
y
1
и еще два одинаковых цилин-
дра радиусом
y
2
; при
α
→
90
◦
y
1
,
y
2
→
y
При
α
≈
α
кр
в остав-
шуюся область входит один цилиндр с максимальным радиусом
z
;
при
α
→
α
кр
z
→
x
. В этом случае в каждую фундаментальную
ячейку попадает часть цилиндра с осью, проходящей через точку O
0
1
,
две одинаковых части цилиндров с осями, проходящими через точки
O
0
2
и O
0
4
и, возможно, часть цилиндра с осью, проходящей через точ-
ки O
0
3
(рис. 14). При этом с уменьшением значения
α
от
90
◦
до
α
кр
доля этой части будет уменьшаться, пока не обратится в ноль, но бу-
дет возрастать неучтенная часть цилиндров, изображенных на рис. 14
пунктиром.
90
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 2


