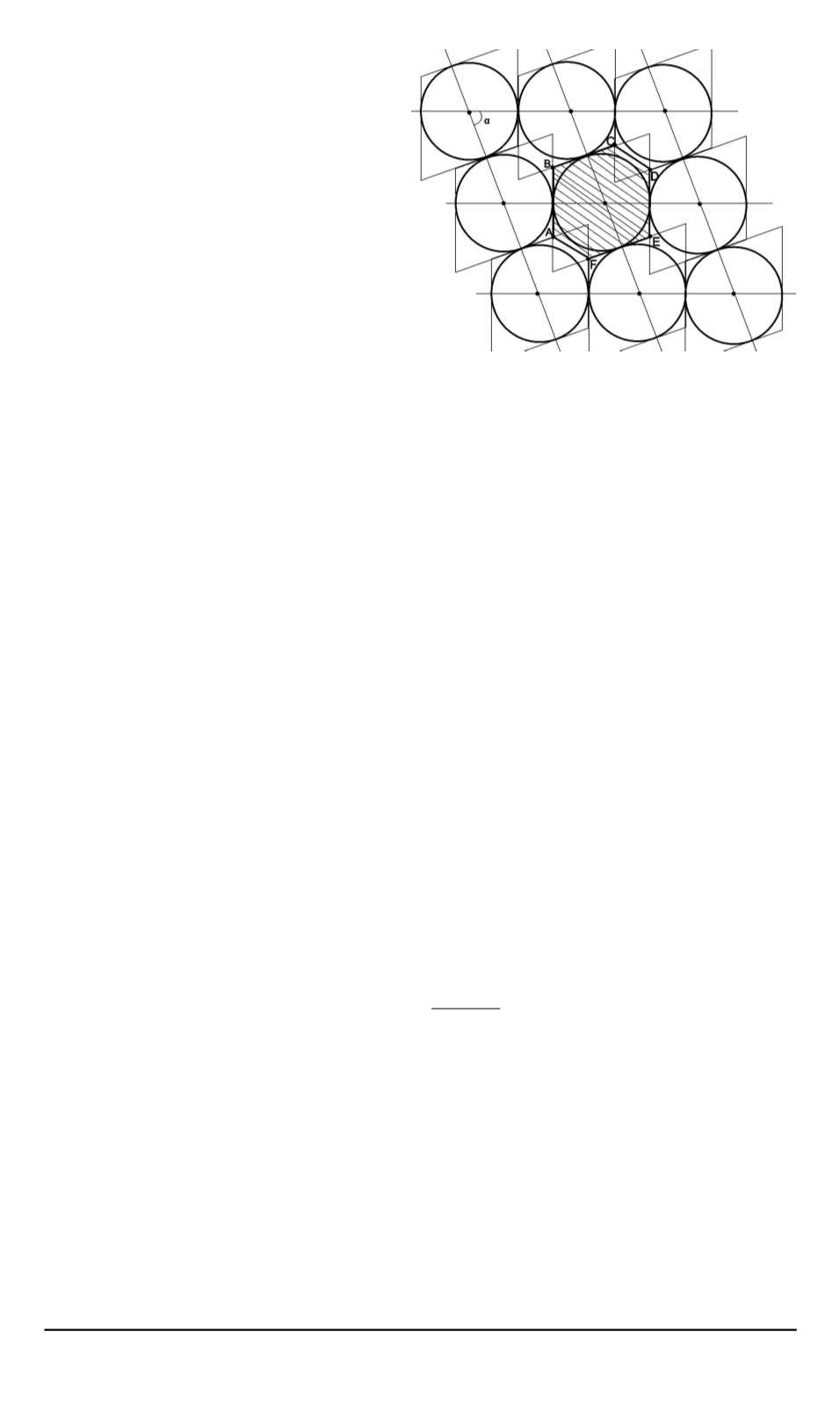
Рис. 1.
Схема упаковки при
60
◦
< α <
90
◦
внешним образом; 3) вычислить
плотность новой упаковки с уче-
том появления цилиндров со-
гласно п. 2; 4) oпределить мак-
симальный радиус прямого кру-
гового цилиндра с основания-
ми на верхней и нижней плос-
костях, касающегося элементов
новой упаковки внешним обра-
зом; 5) вычислить плотность но-
вой упаковки с учетом появле-
ния цилиндров согласно п. 4 и
так далее до тех пор, пока доба-
вление новых цилиндров не будет оказывать существенного влияния
на плотность упаковки; 6) выяснить, при каких значениях
α
плотность
соответствующей упаковки будет наибольшей, т.е. найти оптимальную
упаковку.
Существует несколько принципиально разных подходов к реше-
нию подобных оптимизационных задач. Так, в работах [1, 2] рас-
смотрены математические модели и оптимизационные методы геоме-
трического проектирования, основанные на введенной авторами так
называемой функции плотного размещения. В настоящей статье ис-
пользован подход, близкий к классическому, изложенный, например,
в работах [3, 4].
Рассмотрим систему
{
G
i
}
, содержащую счетное множество одно-
связных фигур (элементов упаковки), расположенных в
n
-мерном про-
странстве произвольным образом; пусть
V
i
— объем элемента
G
i
.
Обычно (см., например, [1], [2]), плотность упаковки определяется
так: выбирается большая шарообразная область, скажем, радиуса
R
;
вычисляется отношение объема элементов упаковки, целиком попав-
ших в эту область, к ее объему, и используется предельный переход
R
→ ∞
:
δ
= lim
R
→∞
P
R
V
i
V
n
(
R
)
,
(1)
где
V
n
(
R
)
— объем
n
-мерного шара радиуса
R
, а
P
R
— знак суммирова-
ния, распространенного на те элементы упаковки
G
i
, которые целиком
попали внутрь шара радиуса
R
с центром в начале координат.
Для расчета плотности упаковки введем понятие фундаментальной
ячейки.
Пусть элементы первоначальной упаковки
{
G
i
}
представляют со-
бой конгруэнтные множества, ограниченные гладкими выпуклыми по-
верхностями. Рассмотрим многогранники, образованные общими ка-
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 2
79


