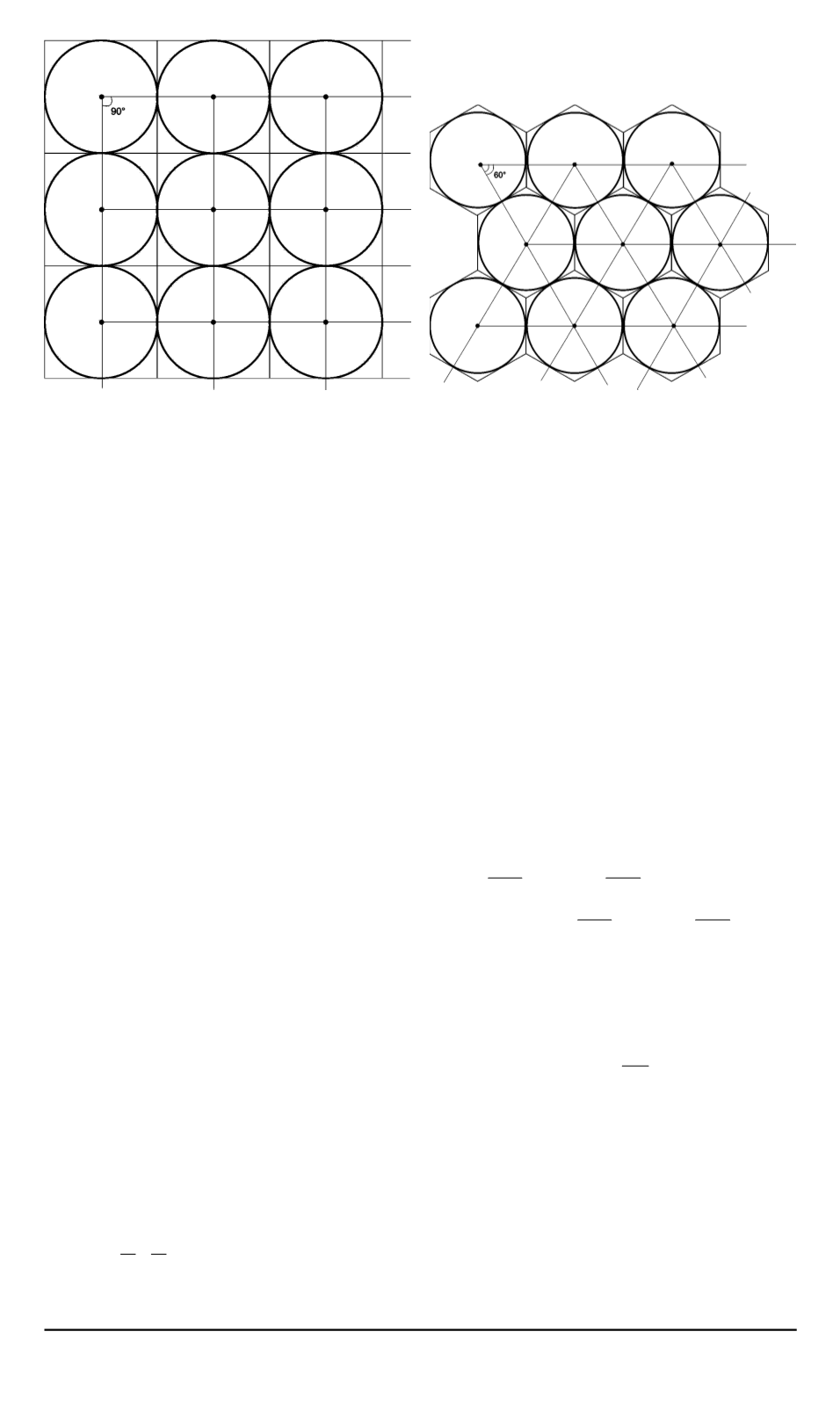
Рис. 2. Схема упаковки при
α
= 90
◦
Рис. 3. Схема упаковки при
α
= 60
◦
сательными плоскостями, проведенными через точки касания двух со-
седних элементов упаковки.
В частности, в случае однослойной упаковки шаров эти плоско-
сти вертикальны, а каждый многогранник представляет собой прямую
призму и является описанным по отношению к соответствующему
шару.
Если эти многогранники не имеют общих внутренних точек, то
каждый из них по определению представляет собой фундаменталь-
ную ячейку, порожденную соответствующим элементом упаковки
(рис. 2; 3).
Если же какой-то многогранник
М
, описанный около некоторого
элемента упаковки, пересекается с соседними
М
1
, . . .
М
k
, как напри-
мер на рис. 1, то фундаментальной ячейкой, порожденной этим эле-
ментом, назовем выпуклую оболочку множества
M
\
(
M
1
∪
. . .
∪
M
k
)
≡
M
∩
M
1
∩
. . .
∩
M
k
:
FC
= Conv [
M
\
(
M
1
∪
. . .
∪
M
k
)]
≡
Conv
M
∩
M
1
∩
. . .
∩
M
k
,
(2)
а так как при
A
∩
B
= 0
A
\
B
=
A
, то в определении фундаментальной
ячейки можно брать
все
многогранники
M
α
, а не только те, у которых
пересечение с многогранником
М
непусто:
FC
= Conv
h
M
\ ∪
α
M
α
i
≡
Conv
h
M
∩ ∩
α
M
α
i
.
(3)
В частности, в случае, изображенном на рис. 1, фундаментальной ячей-
кой является прямая призма с основанием в виде шестиугольника
ABCDEF
и высотой
2
r
.
Прежде чем приступать к изучению случая произвольного
α
2
h
π
3
;
π
2
i
, рассмотрим два частных варианта крайних значений
α
, которые представляют также и самостоятельный интерес.
80
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 2


