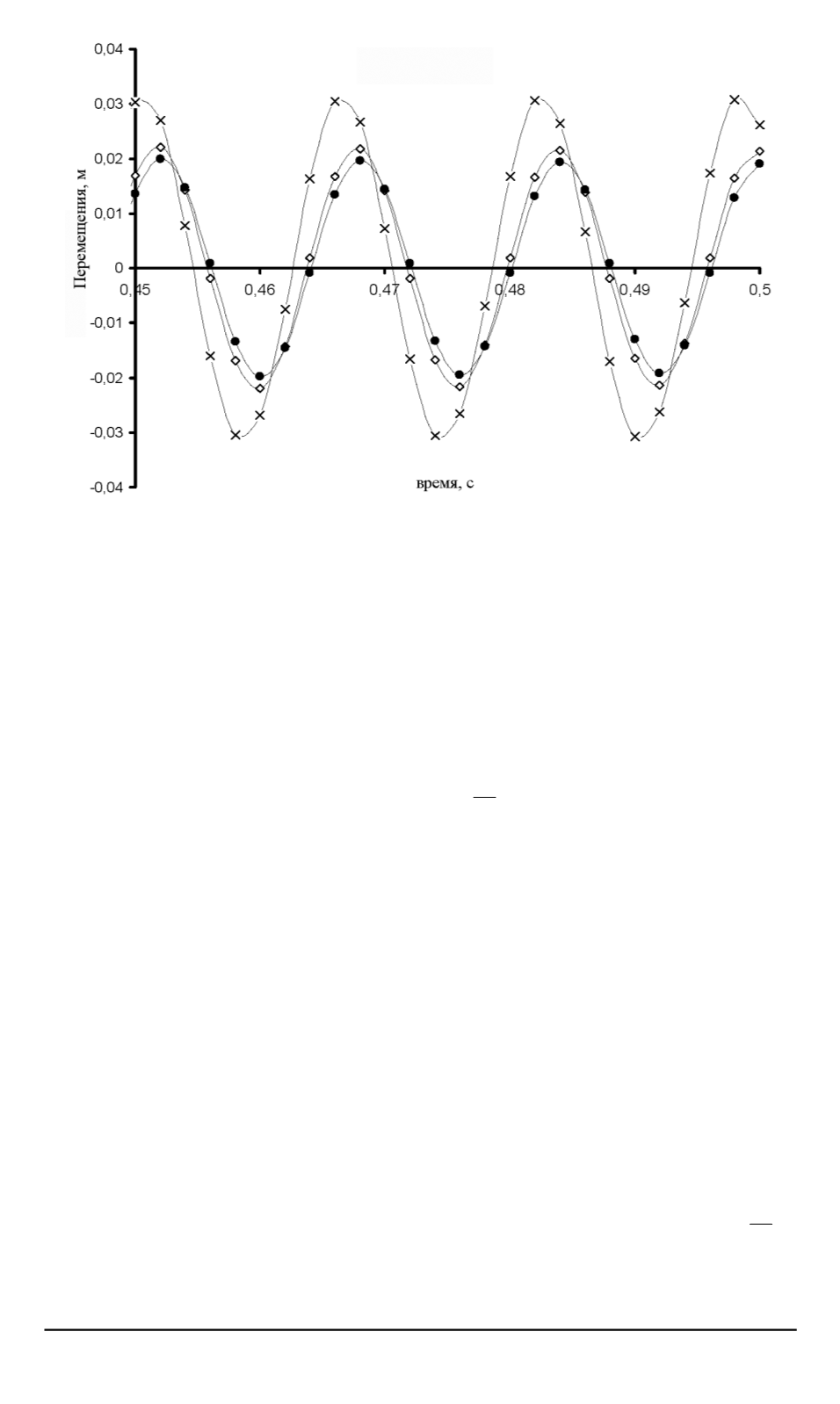
Рис. 2. Зависимость перемещений от времени в случае свободных колебаний:
— численное решение;
•
— прогноз численного решения;
×
— аналитическое
решение
экспериментов даже при относительно больших шагах интегрирова-
ния по времени (
≈
10
% периода). Последнее объясняет значительное
расхождение численного и аналитического решений.
Соотношение (17) проверялось при частоте возбуждения, близкой
к резонансной. Решалась задача о вынужденных колебаниях в главных
координатах. Внешняя нагрузка, приведенная к первой главной коор-
динате, имеет вид
F
1
(
t
) = 1 sin(1
,
01
√
ν
1
t
)
. Внешняя нагрузка, при-
веденная к остальным главным координатам, имеет вид
F
i
(
t
) = 0
,
i
= 2
,
3
, . . . n
. Поперечные перемещения центральной точки пластины
были получены несколькими способами. Во-первых, они были найде-
ны из аналитического решения — график “аналитическое решение” на
рис. 3. Во-вторых, перемещения были получены в численном экспе-
рименте с шагом интегрирования по времени
Δ
τ
= 0
,
001
с — график
“численное решение” на рис. 3. В-третьих, они были найдены по соот-
ношению (17) при
Δ
τ
= 0
,
001
с — график “прогноз численного реше-
ния” на рис. 3. Совпадение результатов, полученных по соотношению
(17) и в численном эксперименте, удовлетворительное.
Соотношение (17) проверялось при частоте возбуждения, значи-
тельно отличающейся от частоты резонанса. Решалась задача о выну-
жденных колебаниях в главных координатах. Внешняя нагрузка, при-
веденная к первой главной координате, имеет вид
F
1
(
t
) = 1 sin(2
√
ν
1
t
)
.
Внешняя нагрузка, приведенная к остальным главным координатам,
имеет вид
F
i
(
t
) = 0
,
i
= 2
,
3
, . . . n
. На рис. 4 приведены поперечные
68
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 1


