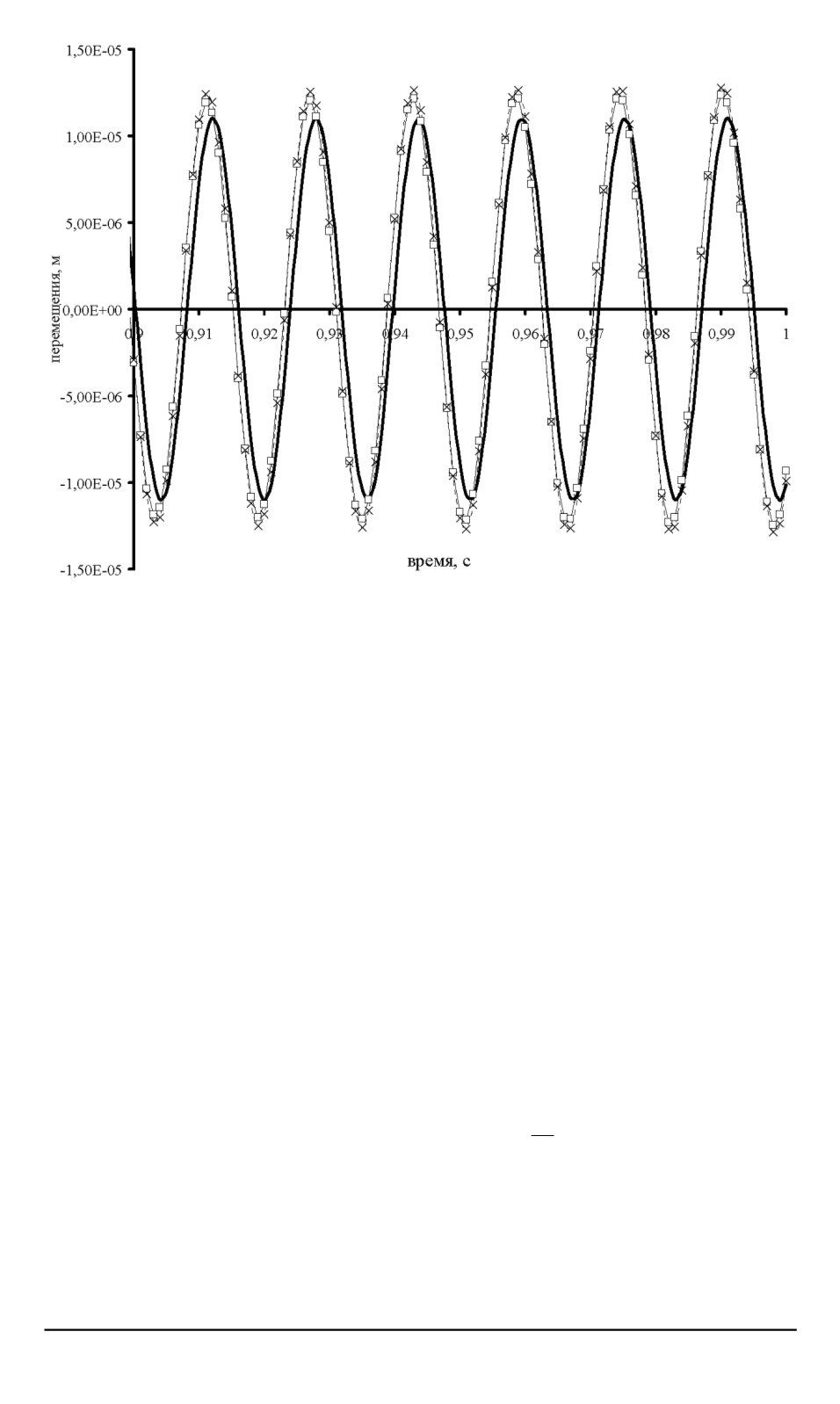
Рис. 3. Зависимость перемещений от времени в случае синусоидальной внешней
нагрузки с частотой, близкой к резонансной:
— численное решение; —— — аналитическлое решение;
×
— прогноз численного
решения
перемещения центральной точки пластины, полученные нескольки-
ми способами. График “аналитическое решение” показывает переме-
щения, которые были найдены из аналитического решения. Графики
“численное решение 1” и “численное решение 2” соответствуют пере-
мещениям из численных экспериментов с шагами интегрирования по
времени
Δ
τ
= 0
,
001
с и
Δ
τ
= 0
,
0001
с соответственно. По соотноше-
нию (17) для
Δ
τ
= 0
,
001
с и
Δ
τ
= 0
,
0001
с были построены графики
“прогноз численного решения 1” и “прогноз численного решения 2”
соответственно. Из представленных на рис. 4 результатов видно удо-
влетворительное соответствие соотношения (17) численному экспери-
менту в широком диапазоне шагов интегрирования по времени.
Соотношение (20) проверялось при частоте возбуждения, равной
резонансной частоте. Решалась задача о вынужденных колебаниях в
главных координатах. Внешняя нагрузка, приведенная к первой глав-
ной координате, имеет вид
F
1
(
t
) = 1 sin(
√
ν
1
t
)
. Внешняя нагрузка,
приведенная к остальным главным координатам, имеет вид
F
i
(
t
) = 0
,
i
= 2
,
3
, . . . n
. Поперечные перемещения центральной точки пласти-
ны были получены, во-первых, из аналитического решения — гра-
фик “аналитическое решение” на рис. 5. Во-вторых, в численных экс-
периментах с шагами интегрирования по времени
Δ
τ
= 0
,
001
с и
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 1
69


