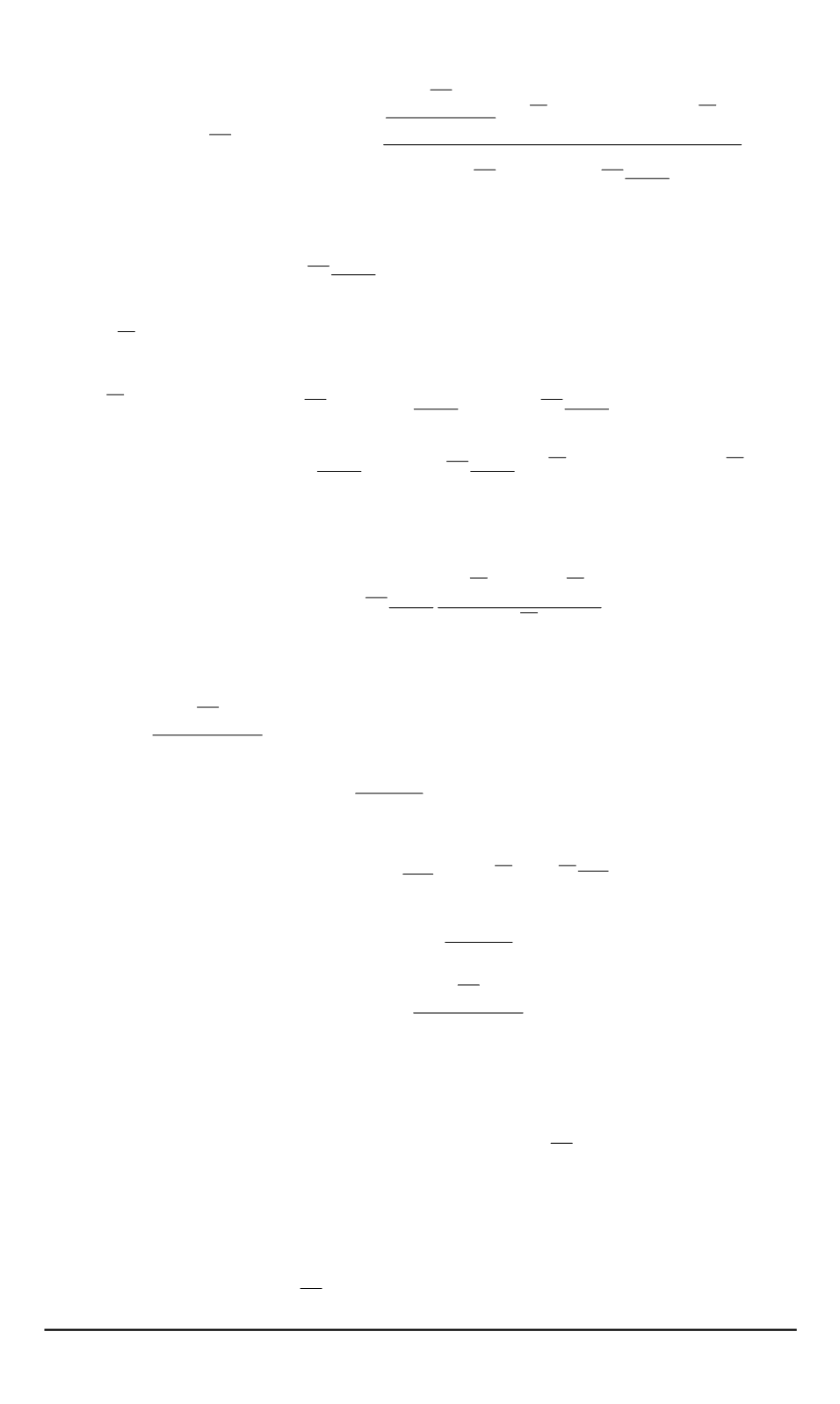
e
i
Δ
w
Δ
τ
= 1 +
i
Δ
w
Δ
τ
. Тогда будет справедливо соотношение
De
i
Δ
wt
k
=
i
√
ν
j
Ce
i
Δ
wt
k
1
−
ν
2
j
√
ν
j
Δ
τ
5
120
e
i
√
ν
j
ξ
1
+ Δ
w
Δ
τ e
i
√
ν
j
Δ
τ
√
ν
j
Δ
τ
−
ν
j
√
ν
j
Δ
τ
3
6
.
В знаменателе дроби пренебрегли слагаемыми высшего порядка ма-
лости относительно
ν
j
√
ν
j
Δ
τ
3
6
. Подстановка полученного выражения
в первое уравнение системы (10) и сокращение правой и левой частей
на
e
i
(
√
ν
j
+Δ
w
)
t
k
приводит к уравнению
e
i
(
√
ν
j
+Δ
w
)
Δ
τ
= 1 +
i
√
ν
j
Δ
τ
−
ν
j
Δ
τ
2
2
−
iν
j
√
ν
j
Δ
τ
3
6
+
+
ν
2
j
Δ
τ
4
24
−
iν
2
j
√
ν
j
Δ
τ
5
120
e
i
√
ν
j
ξ
1
−
i
Δ
w
Δ
τ e
i
√
ν
j
Δ
τ
,
которое с использованием формулы Лагранжа для остатка ряда позво-
ляет получить соотношение для
Δ
w
:
Δ
w
=
−
ν
2
j
√
ν
j
Δ
τ
4
120
e
i
√
ν
j
ξ
1
+
e
i
√
ν
j
ξ
2
2
e
i
√
ν
j
Δ
τ
,
(11)
где
ξ
2
2
[0
,
Δ
τ
]
. Из равенства (11) видно, что в первом приближении
действительная часть
Δ
w
отрицательна и по модулю не превышает
значения
ν
2
j
√
ν
j
Δ
τ
4
120
, а мнимая часть
Δ
w
положительна и по моду-
лю не превышает значения
ν
3
j
Δ
τ
5
120
. Отсюда следуют выражение для
численного решения и предельные значения погрешностей:
q
k
=
q
(
t
k
) =
Ce
−
ν
3
j
Δ
τ
5
120
t
k
e
i
√
ν
j
−
ν
2
j
√
ν
j
Δ
τ
4
120
t
k
,
(12)
Δ
амплитуды
=
ν
3
j
Δ
τ
5
120
t,
(13)
Δ
частоты
=
ν
2
j
√
ν
j
Δ
τ
4
120
t.
(14)
Помимо того, ошибки в определении амплитуды и фазы полу-
чаемого решения могут появиться при записи конечно-разностной
схемы (8) для первого шага интегрирования по времени. Если ана-
литическое решение имеет вид
q
=
C
0
cos(
√
ν
j
t
+
δ
0
)
, а численное
q
k
=
q
(
t
k
) =
C
1
cos(
μt
k
+
δ
1
)
, то будет справедливым записать началь-
ные условия (для
t
=
t
0
= 0)
(
C
0
cos(
δ
0
) =
C
1
cos(
δ
1
)
,
√
ν
j
C
0
sin(
δ
0
) =
μC
1
sin(
δ
1
)
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 1
63