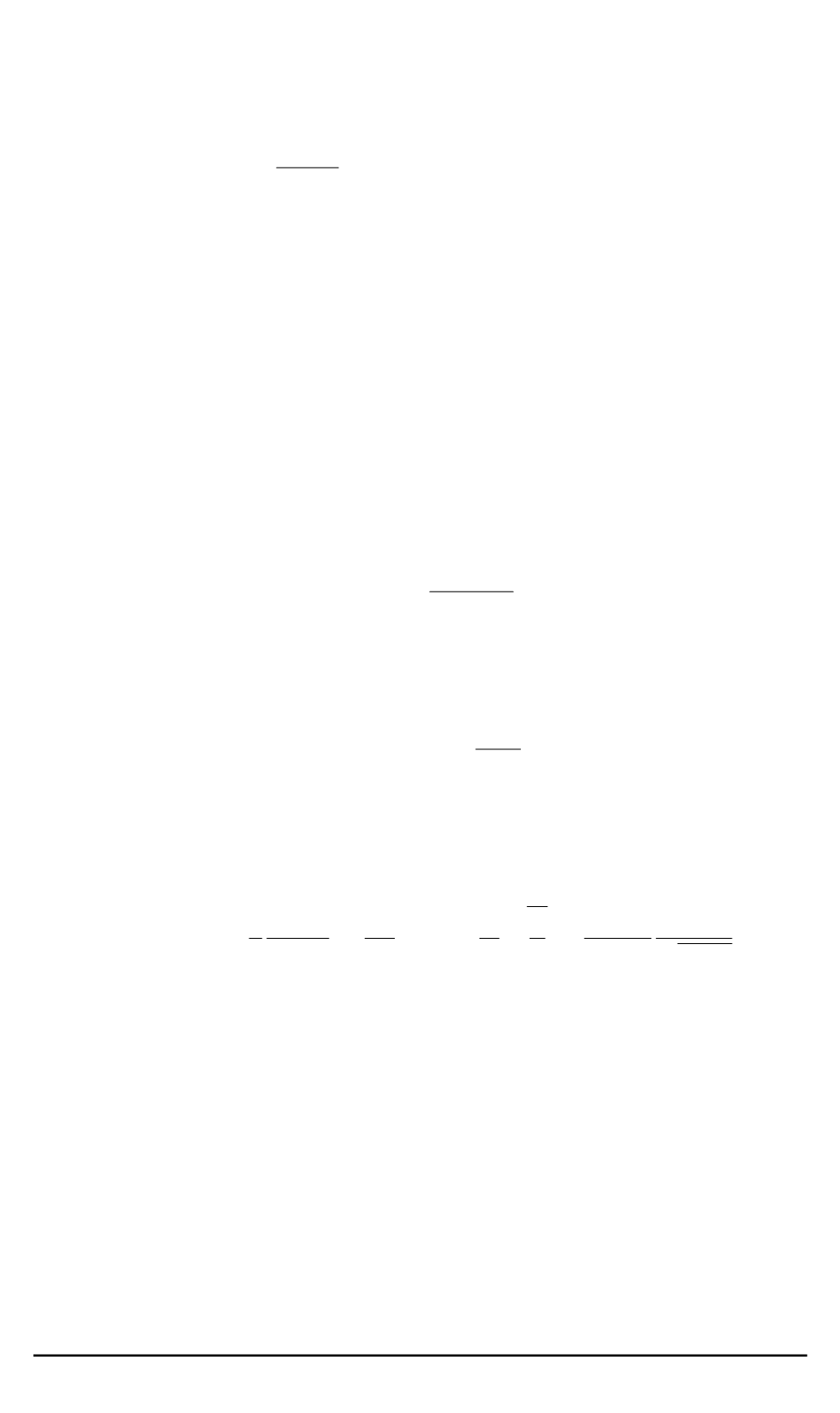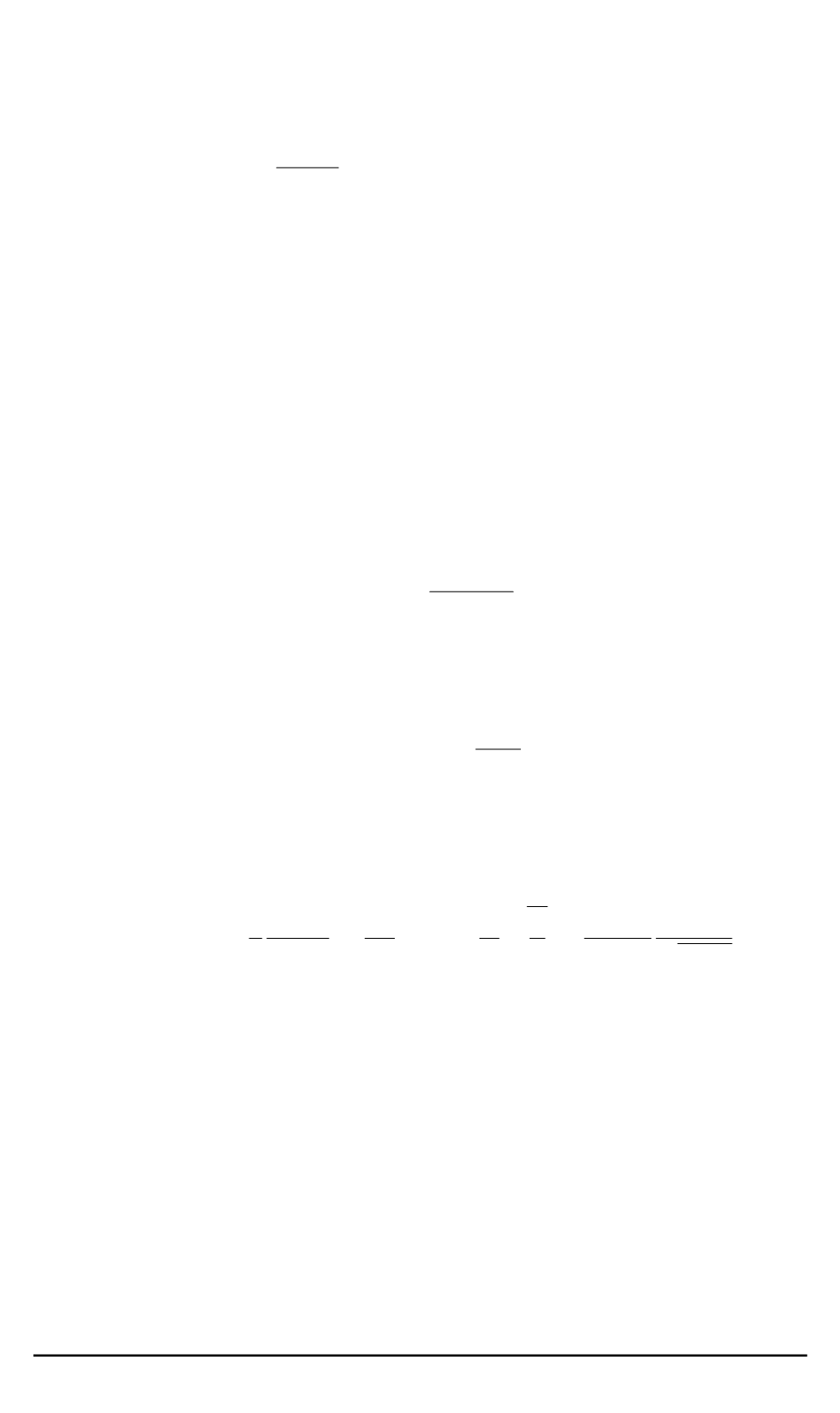
где
F
c
(
t
)
— сила сопротивления,
F
0
(
t
)
— сумма остальных внешних
заданных сил.
Уравнение (1) с учетом выражения (2) примет вид
M
dV
(
t
)
dt
=
F
0
(
t
) +
F
c
(
t
) +
ξ
(
t
)
.
(3)
Когда случайное воздействие
ξ
(
t
)
является производной от про-
цесса с независимыми приращениями (например, представляет собой
белый гауссов шум), а сила сопротивления
F
c
(
t
) =
F
c0
(
t
)
записывается
в виде
F
c0
(
t
) =
−
γV
(
t
)
,
(4)
где
γ
— коэффициент вязкого трения, то скорость частицы
V
(
t
)
опи-
сывается марковским случайным процессом, вследствие чего для нее
можно определить любые
L
-мерные характеристические функции, а
значит, и любые
L
-мерные функции распределения [6]. Такой подход
приводит, в частности, к следующей функции спектральной плотности
для флуктуаций скорости частицы
V
(
t
)
[4]:
G
V
(
ω
) =
α
ω
2
+
β
2
,
(5)
где
α
= 2
γkT/M
2
,
β
=
γ/M
и для шарообразной частицы
γ
= 6
πρνR
.
Для низких частот спектральная плотность
G
V
(
ω
)
стремится к посто-
янной величине:
G
V
(
ω
)
ω
→
0
=
2
kT
γ
.
(6)
Однако, как показано в работе [5], в случае движения частицы в
неограниченной вязкой среде, соотношение для силы сопротивления
имеет вид
F
c
(
t
) =
−
2
πρR
3
1
3
dV
(
t
)
dt
+
3
ν
R
2
V
(
t
) +
3
R
r
ν
π
t
Z
0
dV
(
τ
)
dτ
dτ
√
t
−
τ
.
(7)
В последнем выражении момент времени
t
= 0
принят за начало дви-
жения частицы. На рис. 1 показаны графики функций
F
c0
(
t
)
и
F
c
(
t
)
.
При этом принято, что
V
(
t
) =
V
0
cos(2
πt
)
,
V
0
= 1
м/с. Из графиков хо-
рошо видно существенное отличие сил сопротивления, описываемых
выражениями (4) и (7).
На рис. 2 изображена зависимость силы сопротивления (7) от ско-
рости частицы при
t
→ ∞
для разных
R
, причем
V
(
t
) =
V
0
cos(2
πt
)
,
V
0
= 1
м/с,
ν
= 10
−
6
м
2
/с,
ρ
= 10
3
кг/м
3
. Легко видеть, что график зави-
симости
F
c
(
V
)
имеет вид, напоминающий петлю гистерезиса для маг-
нитного материала на участке линейной намагниченности, зеркально
отображенной относительно оси скоростей.
4
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4