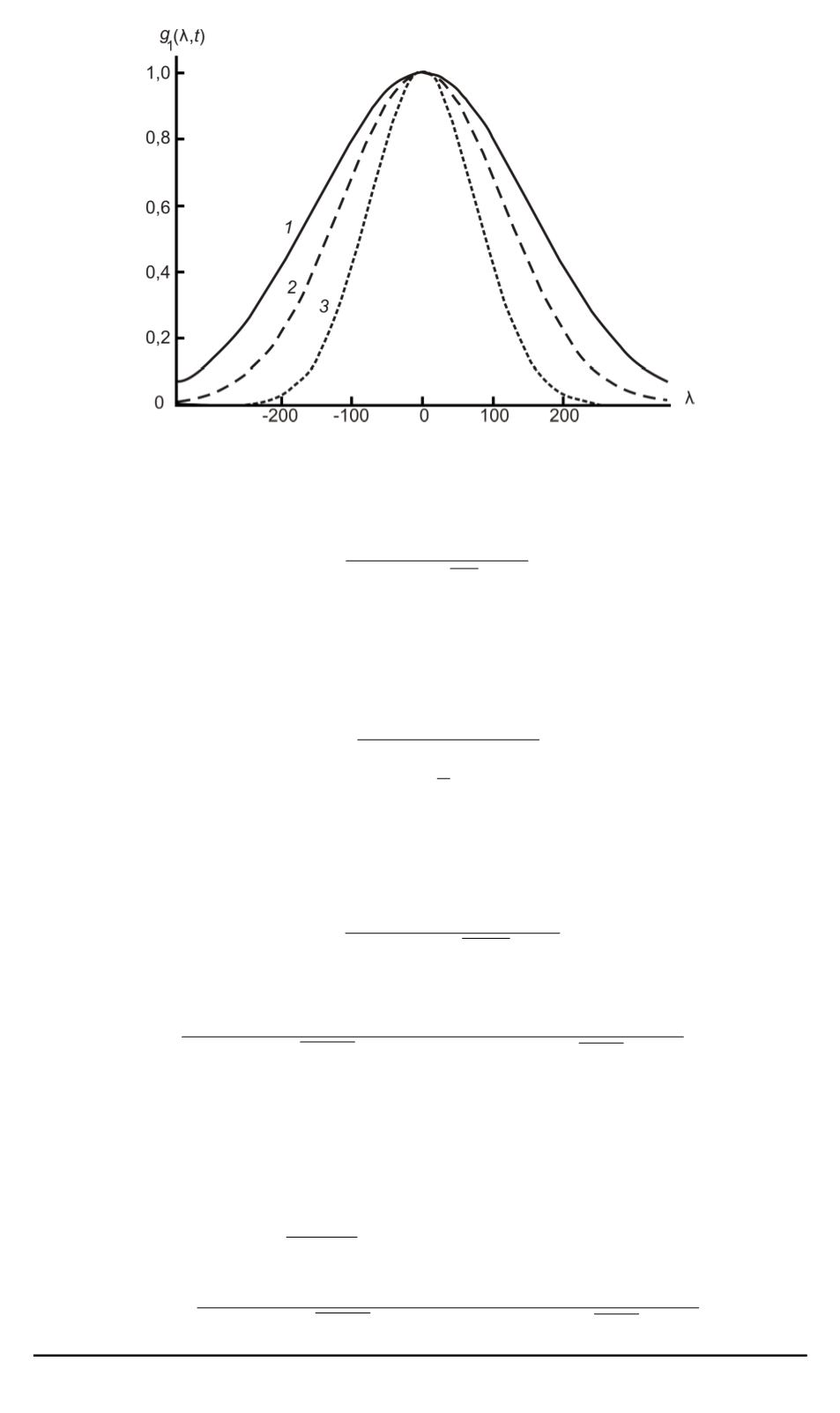
Рис. 4. График функции
g
1
(
λ
;
t
)
при
˜
σ
= 0
,
5
м
2
/с
3
,
А
= 0
,
01
с
−
1
,
В
= 0
,
1
с
1
/
2
,
t
= 0
,
01
с (
1
),
t
= 0
,
1
с (
2
),
t
= 0
,
5
с (
3
)
или
ˆ
Z
(
p
) =
p
p
+
AB
√
πp
+
A
ˆ
ξ
(
p
)
,
(27)
где
ˆ
Z
(
p
)
и
ˆ
ξ
(
p
)
— изображения функций
Z
(
t
)
и
˜
ξ
(
t
)
соответственно.
В связи с тем, что спектральная плотность
G
˜
ξ
= ˜
σ
процесса
˜
ξ
(
t
)
постоянна и равна
G
˜
ξ
=
12
πρνRkT
M
+
2
3
πρR
3
2
,
(28)
то в соответствии с формулой (27) спектральная плотность процесса
Z
(
t
)
при
t
→ ∞
принимает вид
G
Z
(
ω
) =
iω
iω
+
AB
√
π
∙
iω
+
A
2
G
˜
ξ
(29)
или
G
Z
(
ω
) =
ω
2
ω
2
+
AB
√
2
πω
3
+
A
2
B
2
πω
+
A
2
B
√
2
πω
+
A
2
G
˜
ξ
.
(30)
На рис. 5 приведены графики спектральных плотностей для раз-
личных значений
A
и
G
˜
ξ
= 1
м
2
/с
3
, задаваемые формулой (30).
Из последнего выражения может быть найдена спектральная плот-
ность флуктуаций скорости броуновской частицы
V
(
t
)
. Согласно вы-
ражению (9)
G
V
(
ω
) =
G
Z
(
ω
)
ω
2
или
G
V
(
ω
) =
G
˜
ξ
ω
2
+
AB
√
2
πω
3
+
A
2
B
2
πω
+
A
2
B
√
2
πω
+
A
2
.
(31)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4
9


