K
3
(
t, τ
) =
=
A
3
1
2
(
t
−
τ
)
2
+ 4
B
(
t
−
τ
)
3
/
2
+ 3
πB
2
(
t
−
τ
) + 2
πB
3
(
t
−
τ
)
1
/
2
,
(18)
K
4
(
t, τ
) =
−
A
4
1
6
(
t
−
τ
)
3
+
32
15
B
(
t
−
τ
)
5
/
2
+ 3
πB
2
(
t
−
τ
)
2
+
+
16
3
πB
3
(
t
−
τ
)
3
/
2
+
π
2
B
4
(
t
−
τ
)
.
(19)
Из выражений (16)–(19) видно, что ряд (14) является знакочере-
дующимся, причем резольвента
R
(
t, τ
)
является функцией только от
разности аргументов:
R
(
t, τ
) =
R
(
t
−
τ
)
.
Из (16)–(19) следует также,
что абсолютные значения членов ряда (за исключением первого) воз-
растают при росте
t
−
τ
таким образом, что
|
K
n
(
t
−
τ
)
| → ∞
при
(
t
−
τ
)
→ ∞
.
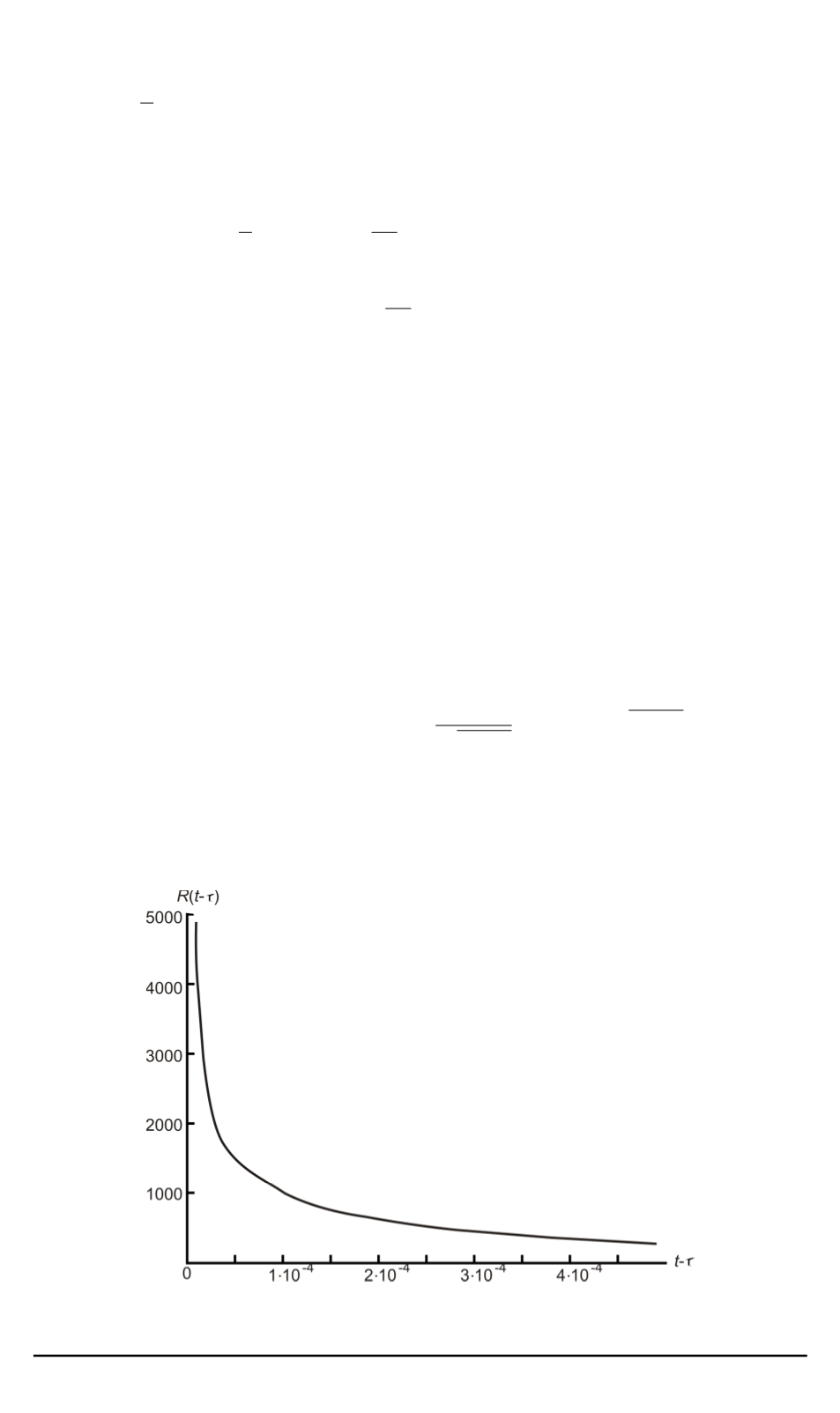
График функции
R
(
t
−
τ
)
(для первых четырех членов)
при
A
= 250
c
−
1
и
B
= 0
,
05
с
1
/
2
показан на рис. 3. Видно, что график
быстро стремится к нулю с ростом
t
−
τ
. Для не слишком больших
t
(
t
≤
10
c) и
А
1
с
−
1
ряд (14) с большой степенью точности можно
заменить следующей суммой:
R
(
t
−
τ
) =
A
−
πA
2
B
2
+
AB
√
t
−
τ
−
4
BA
2
√
t
−
τ .
(20)
Свободная частица.
Будем далее считать, что
˜
F
0
(
t
) = 0
. В этом
случае выражение (13) примет вид
Рис. 3. График функции
R
(
t
−
τ
)
−
(для первых четырех членов) при
A
= 250
c
−
1
и
B
= 0
,
05
,
с
1
/
2
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4
7


